ここが変だよ算数教育【長方形と正方形】 [算数教育の話]
今日の出来事です。
ある先生が算数のテストの丸付けをしていたのですが,その中に次のような問題がありました。
いくつか四角形がかかれており,
「図の中から,次の形を選びましょう。」
「1.正方形」
「2.長方形」
図の中には正方形や長方形,それ以外の四角形が8つほどかかれていて,それぞれア~クまで記号がふられていました。
エはいわゆる正方形だったのですが,私はその先生にこう聞きました。
「エだって長方形じゃない?」
すると「エは正方形ですよね?」と言うので,
「だってエの四角形は4つの角が全部直角になってるよね? 長方形って,4つの角がみな直角な四角形なんだから,エだって長方形だよ?」
と教えたところ,若干考えた後に,
「あ~,そう言われればそうですね!」
教科書にだって,長方形の定義には角が4つとも直角になっていれば良いと書かれているのだから,何で正方形も長方形に選んではいけないのか,明らかにおかしいのです。
明らかにおかしいのに,日本の教員はそれに気づいていない人が多い。
私としては,教員に責任はないと思います。
数学が得意な人ばかりではないからです。
私だったら,逆に社会や国語は苦手なので,教科書におかしな事が書いてあったとしても,それを信じるしかないですからね。
責任があるとすれば,日本の教育出版社や,文部科学省なのだと思います。
先日,文部科学省の数学離れがテレビ番組でも取り上げられていましたが,ちゃんと数学を理解している人がそもそも少ないのではないかと思います。
念のために言うと,私は別に文系の人を馬鹿にしているわけではありません。
文系科目が得意な人は得意な人で,理系の人が知らないような知識や教養や豊かな感性を身に着けているでしょうし。
算数教育全体でも数学離れは進んでいるような気がしています。
いわゆる,
「算数は得意だけど,数学は全然分からない」
という人ですね。
そういった人たちは,算数の中だけで話が全て完結してしまっていますから,集合論的な発想は必要ないのです。
なので,集合的に正方形が長方形の部分集合であるという見方をそもそもしていないのです。
全員がそうというわけではありませんが,気づいていたとしても,算数教育全体がそのようなおかしな問題を放置してしまっているので,どうしようもないといったところが本当のところだと思います。
ある先生が算数のテストの丸付けをしていたのですが,その中に次のような問題がありました。
いくつか四角形がかかれており,
「図の中から,次の形を選びましょう。」
「1.正方形」
「2.長方形」
図の中には正方形や長方形,それ以外の四角形が8つほどかかれていて,それぞれア~クまで記号がふられていました。
エはいわゆる正方形だったのですが,私はその先生にこう聞きました。
「エだって長方形じゃない?」
すると「エは正方形ですよね?」と言うので,
「だってエの四角形は4つの角が全部直角になってるよね? 長方形って,4つの角がみな直角な四角形なんだから,エだって長方形だよ?」
と教えたところ,若干考えた後に,
「あ~,そう言われればそうですね!」
教科書にだって,長方形の定義には角が4つとも直角になっていれば良いと書かれているのだから,何で正方形も長方形に選んではいけないのか,明らかにおかしいのです。
明らかにおかしいのに,日本の教員はそれに気づいていない人が多い。
私としては,教員に責任はないと思います。
数学が得意な人ばかりではないからです。
私だったら,逆に社会や国語は苦手なので,教科書におかしな事が書いてあったとしても,それを信じるしかないですからね。
責任があるとすれば,日本の教育出版社や,文部科学省なのだと思います。
先日,文部科学省の数学離れがテレビ番組でも取り上げられていましたが,ちゃんと数学を理解している人がそもそも少ないのではないかと思います。
念のために言うと,私は別に文系の人を馬鹿にしているわけではありません。
文系科目が得意な人は得意な人で,理系の人が知らないような知識や教養や豊かな感性を身に着けているでしょうし。
算数教育全体でも数学離れは進んでいるような気がしています。
いわゆる,
「算数は得意だけど,数学は全然分からない」
という人ですね。
そういった人たちは,算数の中だけで話が全て完結してしまっていますから,集合論的な発想は必要ないのです。
なので,集合的に正方形が長方形の部分集合であるという見方をそもそもしていないのです。
全員がそうというわけではありませんが,気づいていたとしても,算数教育全体がそのようなおかしな問題を放置してしまっているので,どうしようもないといったところが本当のところだと思います。
角柱・円柱の体積の誤解【なぜ底面積×高さなのか?】 [算数教育の話]
小学校の算数で,特に算数が得意で塾などですでに角柱・円柱の体積の公式を学習している子どもに多い勘違いがあります。
角柱・円柱の体積=底面積×高さ
なのですが,なぜ底面積×高さで求められるのでしょうか?
と問うと,大体が誤った説明をしています。
どういった理解かというと,例えば円柱であれば,
「円形の紙を積み重ねると円柱ができるから」
「底面は円だから,それを高さの分だけ引き伸ばしてやれば,体積になるから」
といった理解の仕方です。
例えば,円盤のCDは一枚一枚は薄くても,それを積み重ねれば高さが出来て円柱になるようなイメージですね。
これは何となく積分の考えに通じるものがありますが,実はこの考えでは正しく円柱の体積がなぜ「底面積×高さ」で求められるのかの説明にはなっていません。
なぜなら,いくら円柱を薄く輪切りにしたところで,それら1つひとつは「厚みの薄い円柱」に変わりないからです。
下の図を見てください。
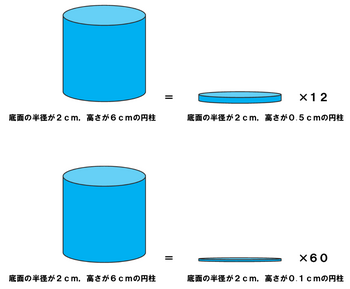
これは,底面の半径が2cm,高さが6cmの円柱を,0.5cmと0.1cmの厚みの輪切りにした図です。それぞれの場合で円柱の体積を求める式を考えてみます。(円周率は3.14とします)
(1)厚み0.5cmの輪切りにした場合,その輪切り12個分が元の円柱の体積なので,
(2×2×3.14×0.5)×12=75.36
(2)厚み0.1cmの輪切りにした場合,その輪切り60個分が元の円柱の体積なので,
(2×2×3.14×0.1)×60=75.36
気づきましたでしょうか?
式中で青くした部分に注目してもらいたいのですが,いくら厚みを薄くしたところで,その輪切り1つひとつの体積を求めるときに「底面積×高さ」を使っているのです。
なぜ円柱の体積は「底面積×高さ」で求められるのかを説明するのに,「円柱の体積=底面積×高さ」という公式を使ってしまっているのです。
説明したい事柄を説明の中で使ってしまっては,説明になりませんね。
このように,「円柱を薄い円盤が積み重なったもの」と見ても,それは「底面積×高さ」で体積が求められることの説明にはならないのです。
ただし,こんなことを小学生に説明したとしても,ほとんどの子は理解できませんよね。
なので小学校の教科書にも円柱の体積の公式に関しては何となくはぐらかしたような書き方をしているのです。
しかし,角柱・円柱の体積の公式は小学校で習ってそれ以降はきちんと考える機会がほとんどないため,大人でも大多数の人は何となく「底面積×高さ」という公式を知っているだけで,その公式の説明(証明)は難しいのではないでしょうか?
同じようなことが円の面積の公式でも言えますね。
円の面積の公式「半径×半径×円周率」も小学校で習いますが,小学校でしか習わないので大人になってもなぜ円の面積の公式が成り立つのか,きちんと説明することは難しいのです。
話を角柱・円柱の体積に戻しますが,上のように輪切りにしてその体積を求める考え方は,公式の説明には適しませんでしたが,考え方自体は数学的には重要な考え方です。
例えば角錐や円錐,回転体のように,輪切りにした時に断面の面積が変化するような立体の体積を求めるときには有効な考え方ですね。
それこそ積分をして体積を求めることが必要になりますからね。
角柱・円柱の体積=底面積×高さ
なのですが,なぜ底面積×高さで求められるのでしょうか?
と問うと,大体が誤った説明をしています。
どういった理解かというと,例えば円柱であれば,
「円形の紙を積み重ねると円柱ができるから」
「底面は円だから,それを高さの分だけ引き伸ばしてやれば,体積になるから」
といった理解の仕方です。
例えば,円盤のCDは一枚一枚は薄くても,それを積み重ねれば高さが出来て円柱になるようなイメージですね。
これは何となく積分の考えに通じるものがありますが,実はこの考えでは正しく円柱の体積がなぜ「底面積×高さ」で求められるのかの説明にはなっていません。
なぜなら,いくら円柱を薄く輪切りにしたところで,それら1つひとつは「厚みの薄い円柱」に変わりないからです。
下の図を見てください。

これは,底面の半径が2cm,高さが6cmの円柱を,0.5cmと0.1cmの厚みの輪切りにした図です。それぞれの場合で円柱の体積を求める式を考えてみます。(円周率は3.14とします)
(1)厚み0.5cmの輪切りにした場合,その輪切り12個分が元の円柱の体積なので,
(2×2×3.14×0.5)×12=75.36
(2)厚み0.1cmの輪切りにした場合,その輪切り60個分が元の円柱の体積なので,
(2×2×3.14×0.1)×60=75.36
気づきましたでしょうか?
式中で青くした部分に注目してもらいたいのですが,いくら厚みを薄くしたところで,その輪切り1つひとつの体積を求めるときに「底面積×高さ」を使っているのです。
なぜ円柱の体積は「底面積×高さ」で求められるのかを説明するのに,「円柱の体積=底面積×高さ」という公式を使ってしまっているのです。
説明したい事柄を説明の中で使ってしまっては,説明になりませんね。
このように,「円柱を薄い円盤が積み重なったもの」と見ても,それは「底面積×高さ」で体積が求められることの説明にはならないのです。
ただし,こんなことを小学生に説明したとしても,ほとんどの子は理解できませんよね。
なので小学校の教科書にも円柱の体積の公式に関しては何となくはぐらかしたような書き方をしているのです。
しかし,角柱・円柱の体積の公式は小学校で習ってそれ以降はきちんと考える機会がほとんどないため,大人でも大多数の人は何となく「底面積×高さ」という公式を知っているだけで,その公式の説明(証明)は難しいのではないでしょうか?
同じようなことが円の面積の公式でも言えますね。
円の面積の公式「半径×半径×円周率」も小学校で習いますが,小学校でしか習わないので大人になってもなぜ円の面積の公式が成り立つのか,きちんと説明することは難しいのです。
話を角柱・円柱の体積に戻しますが,上のように輪切りにしてその体積を求める考え方は,公式の説明には適しませんでしたが,考え方自体は数学的には重要な考え方です。
例えば角錐や円錐,回転体のように,輪切りにした時に断面の面積が変化するような立体の体積を求めるときには有効な考え方ですね。
それこそ積分をして体積を求めることが必要になりますからね。
日常生活に活用できる算数は学力低下の元? [算数教育の話]
最近の算数教育の中で,よく日常生活に算数を役立てる態度を育てるといったことが出てきます。
算数の学習指導要領の中にも非常によく出てくるワードです。
ですがよく考えてみてください。
日常生活で算数をどれだけ使いますか?
割合? 概算? 料理で比?
あとは四則演算(+-×÷)くらいですか。
角柱の体積やら比例・反比例のグラフやら,日常生活のなんの役に立つというのでしょうか。
まぁ,無理矢理役に立つ場面も作れと言われれば作れるかもしれませんが,普段生活している分にはほとんどの算数は使わないでしょう。
数学者の中には「役に立たないからこそ美しい」という方も多いです。
ラマヌジャンを見出したハーディという整数論の分野で活躍した偉大な数学者ですら,自分のしている純粋数学はなんの役にも立たないと豪語していたそうです。
実際は,その理論が戦時中の暗号を作り出すことに一役買ってしまうことになってしまうのですが。
数学の歴史上もっとも美しいと言われているオイラーの公式ですら,日常生活には何の役にも立っていません。
数学というのはあくまで思考の学問です。
つまり実際にあるものを試行錯誤したり実験したりして実証するのではなく,論理的な推論をもとに思考を展開してく学問です。
純粋数学では実験ではなく,すべて証明で話が進んでいきますので,数学の世界で証明されたことは絶対なんですね。
実験ですと,100回の実験で同じ結果が出たとしても,もしかしたら101回目の実験でそれに反する結果が出る可能性もありますが,数学では一度(間違いなく)証明されたことは,何度やってもそうなるのです。
数学を楽しんだり,興味を持ったりするのは,どう考えても日常生活に役に立つからではありません。
「思考そのものを楽しむ」ということが,数学を楽しむということなんだと思います。
日常生活に役に立つものしか勉強しないというのでは,数学ほぼ全てを勉強しなくて良いことになってしまいますね。
とはいえ,算数に限れば日常生活に役に立つことも少なくはないのですが,中学・高校の数学を本当の意味で楽しむ態度を育てるのであれば,小学校の算数においても,日常生活に役立てるというワードは,一刻も早く削除してほしいと個人的に思います。
みなさんは,どう考えていますでしょうか?
算数の学習指導要領の中にも非常によく出てくるワードです。
ですがよく考えてみてください。
日常生活で算数をどれだけ使いますか?
割合? 概算? 料理で比?
あとは四則演算(+-×÷)くらいですか。
角柱の体積やら比例・反比例のグラフやら,日常生活のなんの役に立つというのでしょうか。
まぁ,無理矢理役に立つ場面も作れと言われれば作れるかもしれませんが,普段生活している分にはほとんどの算数は使わないでしょう。
数学者の中には「役に立たないからこそ美しい」という方も多いです。
ラマヌジャンを見出したハーディという整数論の分野で活躍した偉大な数学者ですら,自分のしている純粋数学はなんの役にも立たないと豪語していたそうです。
実際は,その理論が戦時中の暗号を作り出すことに一役買ってしまうことになってしまうのですが。
数学の歴史上もっとも美しいと言われているオイラーの公式ですら,日常生活には何の役にも立っていません。
数学というのはあくまで思考の学問です。
つまり実際にあるものを試行錯誤したり実験したりして実証するのではなく,論理的な推論をもとに思考を展開してく学問です。
純粋数学では実験ではなく,すべて証明で話が進んでいきますので,数学の世界で証明されたことは絶対なんですね。
実験ですと,100回の実験で同じ結果が出たとしても,もしかしたら101回目の実験でそれに反する結果が出る可能性もありますが,数学では一度(間違いなく)証明されたことは,何度やってもそうなるのです。
数学を楽しんだり,興味を持ったりするのは,どう考えても日常生活に役に立つからではありません。
「思考そのものを楽しむ」ということが,数学を楽しむということなんだと思います。
日常生活に役に立つものしか勉強しないというのでは,数学ほぼ全てを勉強しなくて良いことになってしまいますね。
とはいえ,算数に限れば日常生活に役に立つことも少なくはないのですが,中学・高校の数学を本当の意味で楽しむ態度を育てるのであれば,小学校の算数においても,日常生活に役立てるというワードは,一刻も早く削除してほしいと個人的に思います。
みなさんは,どう考えていますでしょうか?
深い学びって?【細水保宏先生のお話から考える】 [算数教育の話]
今教育で,「深い学び」というのがひとつのキーワードになっていますね。
個人的には良い言葉だなと思いますが,いろいろな意味で,教育関係者の中でも捉えられています。
例えば,授業の中で,「あっ,こうすれば良かったんだ」などちょっとした気づきでも,学びが深まったと捉えることもできると言う方もいます。
どうやら,今まで「活動あって学びなし」の授業が目立つようになってきていたので,そこに「学び」を取り入れようとして,「深い学び」という言葉が登場したそうなんですね。
子どもはまあ楽しそうに取り組んでいましたが,学びはありませんでした。といった授業では,これからはだめだということですね(当たり前ですが)。
では,深い学びとは,算数ではどういうことなのか。
以前,算数教育の巨匠,細水保宏先生のお話を聞く機会があり,「深い学び」にはやや消極的な考えをお持ちだったとのことでした。
なぜかというと,「深い」というのは相対的に「深い」「浅い」があるのであって,何をもって「深い」というのか分からないからだそうです。
でも,ひとつ「深い」に基準を設けるならば,
「数学的な本質にどれだけ迫れたか」
ということのようです。
なるほど。例えば,問題を解くだけならば,公式を丸暗記して当てはめればいいだけですが,それだけだと浅い学びということですね。
ただ単に,「そういうことだったのか」といった気づきだけでは,やはり「深い学び」というのはやや抵抗があります。
だって,例えば7×6=42と計算するところを,7×6=42とすれば良かったことに気づけたとしましょう。
はたしてそれが,深い学びになったと言って良いのでしょうか?
単なる計算間違えが数学的な本質とはとても言えませんね。
ただ,問題は教師の方がどれだけ数学的な本質を理解しているか,問われることになっていくのではないかなと,個人的には思っています(笑)
個人的には良い言葉だなと思いますが,いろいろな意味で,教育関係者の中でも捉えられています。
例えば,授業の中で,「あっ,こうすれば良かったんだ」などちょっとした気づきでも,学びが深まったと捉えることもできると言う方もいます。
どうやら,今まで「活動あって学びなし」の授業が目立つようになってきていたので,そこに「学び」を取り入れようとして,「深い学び」という言葉が登場したそうなんですね。
子どもはまあ楽しそうに取り組んでいましたが,学びはありませんでした。といった授業では,これからはだめだということですね(当たり前ですが)。
では,深い学びとは,算数ではどういうことなのか。
以前,算数教育の巨匠,細水保宏先生のお話を聞く機会があり,「深い学び」にはやや消極的な考えをお持ちだったとのことでした。
なぜかというと,「深い」というのは相対的に「深い」「浅い」があるのであって,何をもって「深い」というのか分からないからだそうです。
でも,ひとつ「深い」に基準を設けるならば,
「数学的な本質にどれだけ迫れたか」
ということのようです。
なるほど。例えば,問題を解くだけならば,公式を丸暗記して当てはめればいいだけですが,それだけだと浅い学びということですね。
ただ単に,「そういうことだったのか」といった気づきだけでは,やはり「深い学び」というのはやや抵抗があります。
だって,例えば7×6=42と計算するところを,7×6=42とすれば良かったことに気づけたとしましょう。
はたしてそれが,深い学びになったと言って良いのでしょうか?
単なる計算間違えが数学的な本質とはとても言えませんね。
ただ,問題は教師の方がどれだけ数学的な本質を理解しているか,問われることになっていくのではないかなと,個人的には思っています(笑)
図形の定義の認識のゆがみ [算数教育の話]
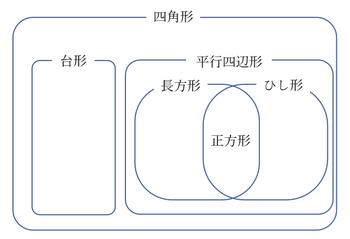
前回、図形を学習する場合には、一般から特殊な図形を学ぶ流れの方が、包摂的な見方が自然に身につくことをお話ししました。
例えば、四角形の中で、
平行な辺の組があれば(少なくとも1組)台形であり、
2組とも平行になっていれば平行四辺形である。
という流れです。さらに、
平行四辺形の中でも辺の長さがみな等しくなっていれば、それはひし形であり、
角がみな直角になっていれば、それは長方形である。
そして、ひし形でもあり長方形でもある形は、正方形である。
このように、一般の形から特殊な形へと少しずつ条件をつけ足していくことで、図形の包摂関係はある程度理解できます。
小学生で多いのが、定義の誤認です。
つまり、本来の図形の定義が何なのか忘れ、本来とは異なる定義の捉え方をしているのです。
例えば、長方形とはどんな形を言うのかと聞けば、多くは、
「角がどこも直角で、辺の長さが縦と横で違うもの」
というふうに言います。
本来の長方形の定義は、
「4つの角がすべて直角になっている四角形」
です。
なぜこのような認識になるのかと言えば、
「辺の長さが同じだったら、正方形になってしまうから」
なのです。
確かに、正方形は長方形とは普通は呼びませんからね。
各図形で呼称がいくつもあっては、小学校低学年の子どもには理解が難しいのです。
学齢が進むごとに、だんだん包摂的な見方もできるようになれば十分なので、その時点では、そのように長方形を理解していても問題はないと思うのですが、問題は教える側の方です。
教える側の教師は、間違っても
「縦と横の長さが違ってないと、長方形じゃないよ」
などと言ってはいけないでしょう。
あくまで正しい定義の仕方で指導しなければ、論理的にいつか破綻します。
学習が進む中で、図形の定義の認識に、本来ないものが付け加わっていくことを、ここでは「定義の認識ゆがみ」と言うことにしましょう。
なぜ、図形は一般から特殊へという流れで学習した方が良いかといえば、定義の認識のゆがみを起こさないためです。
では、特殊から一般の図形へという流れで学習を進めた場合、長方形と正方形を例に、どうなるか説明します。
まず、正方形の定義
「角がみな直角で、辺の長さもみな等しい四角形を正方形といいます」
では次に、長方形の定義
「正方形を横(または縦)に引き伸ばしたような形を長方形といいます」
ここで、「引き伸ばす」ということにより、「縦と横の長さが違う」という条件が、長方形に必要な条件であると認識し、定義の認識のゆがみが生じます。
逆に、特殊から一般へと学習を進めた場合はどうでしょうか。
まず、長方形の定義
「長しかくのように、角がみな直角になっている四角形を長方形といいます」
次に、正方形の定義
「長方形の中でも、辺の長さがどれも同じになっているような真四角の形を正方形といいます」
やはり、定義の認識のゆがみが生じることはないかと思います。
定義の認識のゆがみは、子どもたちの学習の過程である程度はあっても良いとは思いますが、指導する側はこのことを十分に理解して、指導していかなくてはいつか論理的に破綻することになることを良く理解しておかなくてはならないのではないかと思います。
例えば、四角形の中で、
平行な辺の組があれば(少なくとも1組)台形であり、
2組とも平行になっていれば平行四辺形である。
という流れです。さらに、
平行四辺形の中でも辺の長さがみな等しくなっていれば、それはひし形であり、
角がみな直角になっていれば、それは長方形である。
そして、ひし形でもあり長方形でもある形は、正方形である。
このように、一般の形から特殊な形へと少しずつ条件をつけ足していくことで、図形の包摂関係はある程度理解できます。
小学生で多いのが、定義の誤認です。
つまり、本来の図形の定義が何なのか忘れ、本来とは異なる定義の捉え方をしているのです。
例えば、長方形とはどんな形を言うのかと聞けば、多くは、
「角がどこも直角で、辺の長さが縦と横で違うもの」
というふうに言います。
本来の長方形の定義は、
「4つの角がすべて直角になっている四角形」
です。
なぜこのような認識になるのかと言えば、
「辺の長さが同じだったら、正方形になってしまうから」
なのです。
確かに、正方形は長方形とは普通は呼びませんからね。
各図形で呼称がいくつもあっては、小学校低学年の子どもには理解が難しいのです。
学齢が進むごとに、だんだん包摂的な見方もできるようになれば十分なので、その時点では、そのように長方形を理解していても問題はないと思うのですが、問題は教える側の方です。
教える側の教師は、間違っても
「縦と横の長さが違ってないと、長方形じゃないよ」
などと言ってはいけないでしょう。
あくまで正しい定義の仕方で指導しなければ、論理的にいつか破綻します。
学習が進む中で、図形の定義の認識に、本来ないものが付け加わっていくことを、ここでは「定義の認識ゆがみ」と言うことにしましょう。
なぜ、図形は一般から特殊へという流れで学習した方が良いかといえば、定義の認識のゆがみを起こさないためです。
では、特殊から一般の図形へという流れで学習を進めた場合、長方形と正方形を例に、どうなるか説明します。
まず、正方形の定義
「角がみな直角で、辺の長さもみな等しい四角形を正方形といいます」
では次に、長方形の定義
「正方形を横(または縦)に引き伸ばしたような形を長方形といいます」
ここで、「引き伸ばす」ということにより、「縦と横の長さが違う」という条件が、長方形に必要な条件であると認識し、定義の認識のゆがみが生じます。
逆に、特殊から一般へと学習を進めた場合はどうでしょうか。
まず、長方形の定義
「長しかくのように、角がみな直角になっている四角形を長方形といいます」
次に、正方形の定義
「長方形の中でも、辺の長さがどれも同じになっているような真四角の形を正方形といいます」
やはり、定義の認識のゆがみが生じることはないかと思います。
定義の認識のゆがみは、子どもたちの学習の過程である程度はあっても良いとは思いますが、指導する側はこのことを十分に理解して、指導していかなくてはいつか論理的に破綻することになることを良く理解しておかなくてはならないのではないかと思います。
図形の仲間分けはもうやめましょう [算数教育の話]
平行四辺形と台形を学ぶ最初の学習で多く取り入れられている「仲間分け」について、非常に不自然なことをしているのに、そろそろ気づくべきではないでしょうか。
前回の記事での話題とかぶるところもありますが、次の図で、
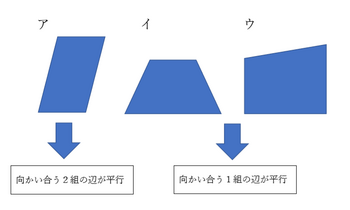
平行な辺が1組ある四角形と、
平行な辺が2組ある四角形に、
分けさせる学習です。この仲間分けに応じて、台形と平行四辺形について、小学4年生の段階で学習します。
仲間分けをさせたらどういうことになるか。
答えは簡単。
平行な辺が2組あったら、それは台形ではないんだ。
と、思い込むに決まっています。
本来、このような仲間分けをするのであれば、元々排他的な2つの対象に対して行うべきです。
例えば、三角形と四角形が混ぜられているのを、三角形と四角形の仲間に分けるなどです。
日本では、少なくとも高校の段階では
平行四辺形も台形の仲間、あるいは台形の中でも特殊な形
と、包摂的にみなすことになっています。
それなのに、なぜ平行四辺形と台形に仲間分けするのか、非常に不自然なことをしているように感じるのです。
例えるならば、あるテストの結果が、
Aくん・・・90点
Bくん・・・60点
Cくん・・・40点
だったとして、
点数が
80点以上の人と、
40点以上の人に
分けましょうと言っているのと同じ。
80点以上であれば、当然40点以上でもあるため、90点だったAくんはどちらにも当てはまる。それなのに「分けろ」というのは無理な話でしょう。
こういった、包摂的な関係にある2つの対象を扱うときには、より一般的な方から集めるのが無難です。
上の例で言えば、
まず、40点以上だった人を集める・・・Aくん、Bくん
次に、80点以上だった人を集める・・・Aくん
というように、まず広い条件で集めてから、さらに特殊な条件を課していくのが自然な流れと言えます。
平行四辺形と台形で言えば、
まず、四角形の中から、向かい合う辺が少なくとも1組は平行になっているものを集める。
次に、向かい合う辺が2組とも平行になっているものを集める。
このように順を追って台形と平行四辺形を学習していくべきです。
一般的なものからより特殊なものへと絞っていくことで、包摂的な見方が自然に育つのではないかと思いますが、より特殊な「正方形」や「長方形」などを混ぜると、子どもによっては混乱するおそれがあります。ですから、子どもによっては、そういった「より特殊な」四角形は除いておくなどの配慮は必要でしょう。
図形の学習で蔓延している「仲間分け」はもうやめにして、このような
仲間集め
の活動で図形の学習をしていくべきではないかと思います。
前回の記事での話題とかぶるところもありますが、次の図で、

平行な辺が1組ある四角形と、
平行な辺が2組ある四角形に、
分けさせる学習です。この仲間分けに応じて、台形と平行四辺形について、小学4年生の段階で学習します。
仲間分けをさせたらどういうことになるか。
答えは簡単。
平行な辺が2組あったら、それは台形ではないんだ。
と、思い込むに決まっています。
本来、このような仲間分けをするのであれば、元々排他的な2つの対象に対して行うべきです。
例えば、三角形と四角形が混ぜられているのを、三角形と四角形の仲間に分けるなどです。
日本では、少なくとも高校の段階では
平行四辺形も台形の仲間、あるいは台形の中でも特殊な形
と、包摂的にみなすことになっています。
それなのに、なぜ平行四辺形と台形に仲間分けするのか、非常に不自然なことをしているように感じるのです。
例えるならば、あるテストの結果が、
Aくん・・・90点
Bくん・・・60点
Cくん・・・40点
だったとして、
点数が
80点以上の人と、
40点以上の人に
分けましょうと言っているのと同じ。
80点以上であれば、当然40点以上でもあるため、90点だったAくんはどちらにも当てはまる。それなのに「分けろ」というのは無理な話でしょう。
こういった、包摂的な関係にある2つの対象を扱うときには、より一般的な方から集めるのが無難です。
上の例で言えば、
まず、40点以上だった人を集める・・・Aくん、Bくん
次に、80点以上だった人を集める・・・Aくん
というように、まず広い条件で集めてから、さらに特殊な条件を課していくのが自然な流れと言えます。
平行四辺形と台形で言えば、
まず、四角形の中から、向かい合う辺が少なくとも1組は平行になっているものを集める。
次に、向かい合う辺が2組とも平行になっているものを集める。
このように順を追って台形と平行四辺形を学習していくべきです。
一般的なものからより特殊なものへと絞っていくことで、包摂的な見方が自然に育つのではないかと思いますが、より特殊な「正方形」や「長方形」などを混ぜると、子どもによっては混乱するおそれがあります。ですから、子どもによっては、そういった「より特殊な」四角形は除いておくなどの配慮は必要でしょう。
図形の学習で蔓延している「仲間分け」はもうやめにして、このような
仲間集め
の活動で図形の学習をしていくべきではないかと思います。
台形と平行四辺形【日本とアメリカの比較】 [算数教育の話]
日本の図形の学習において、多く取り入れられている手法で
「なかま分け」
というものがある。
つまり、ある観点からいくつかの図形を「なかま分け」するのである。
平行四辺形と台形の学習においても、多くの教科書が「なかま分け」を取り入れている。
では、実際にどのような流れで学習が進められるか見ていこう。
(著作権の関係で問題があるかもしれないので、教科書の画像をそのまま載せることは避けるが、流れは全く同じである)
○日本の教科書の場合
1.まず、いくつかの図形をから、同じなかまに分けるところから始まる。平行な辺の組がいくつあるかで、まず図形を弁別する。

2.台形と平行四辺形の定義をする。
「向かい合う1組の辺が平行な四角形を、台形といいます」
「向かい合う2組の辺が平行な四角形を、平行四辺形といいます」
このように、多くの教科書では台形と平行四辺形を弁別することにより、同時に台形と平行四辺形を学習することになっている。
小学生にとっては、確かに、平行四辺形と台形は全く別の図形であると認識した方が、分かりやすいといえば分かりやすいのである。きわめつけで、例えば『教育出版 小学算数4年下』では、次のような問題できちんと理解しているか、確かめるようになっている。
3.次の図形から、台形と平行四辺形を選びましょう。
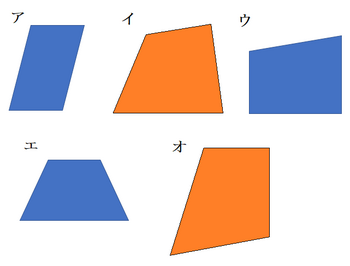
(色分けしているが、特に意味はない)
なかま分けで学習が進んできたため、多くの児童は、
台形・・・ウ,エ
平行四辺形・・・ア
というように考える。
教師用の答えの載っている教科書(通称、朱書き教科書)にも、実際上のような解答になっている。
しかし、ここで問題が生じる。
これは、実際にあったことなのだが、ある児童が、
「平行四辺形(ア)も台形じゃないんですか?」
と、質問したのである。
すると先生はなんと答えたかというと、
「アは平行四辺形なんだから、台形じゃないよ」
である。
その質問をした子は、「平行四辺形だって1組は平行な辺があるんだから、台形のなかまじゃないか」と考えて質問したのに対し、なんともトンチンカンな回答を先生がしてしまっていたのだ。
それでも、その子は引き下がらずに、
「平行四辺形だって1組は平行だから・・・」
と続けたのに対し、先生は
「1組だけ平行じゃないと、台形っていわないよね」
と、押し切ったのだ。
日本の多くの教科書では、「なかま分け」により平行四辺形と台形を弁別しているため、暗に台形の定義が「向かい合う辺が1組だけ平行な四角形」と認識されるように仕組まれているのである。
それはそれで構わないかと思うのだが、問題は5年生になってから、教科書に次のようなベン図がかかれているのである。
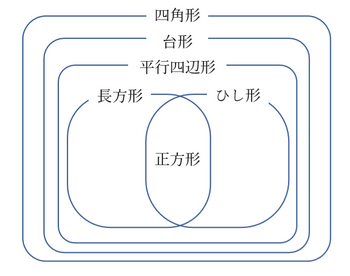
さあ、あの時先生は、「平行四辺形は台形じゃない」と言ったはずなのに、この図はそうなっていないじゃないか!
ここで、教師は手の平を反すしかなくなる。
「実は、平行四辺形も台形のなかまだったんだ」
この問題について、教育出版に直接問い合わせたところ、
「4年生の段階では、平行四辺形は平行四辺形、台形は台形として学習した方が分かりやすいのでこのようになっていますが、5年生になってからは、平行四辺形も台形のなかまとして見る見方があるんだということに気づければ良いのではないかと思います」
といった内容の返事があった。つまり、
分かりやすければ矛盾することになっても仕方がない
ということだろう。
では、4年生の段階で包摂的な見方で「平行四辺形も台形のなかまではないか?」と考えた子の気持ちはどうなってしまうのだろうか?
より発展的な包摂的な考え方をしたのに、ダメだと言われるのである。
こんなことはあってはならないと思うのだが、実際に教育現場ではそのようなことが行われているのである。
○アメリカの教科書の場合
アメリカの小学校で多く使われている『Houghton Mifflin Math』において、台形と平行四辺形は4年生の教科書に、次のように定義されている。なお、日本とは異なり、「なかま分け」は行っていない。
Trapezoid (台形): A trapezoid has only one pair of parallel sides.
Parallelogram (平行四辺形): A parallelogram has opposite sides parallel and of the same length.
ここで、台形の定義で「only」が使われていることに注目したい。
定義の段階ではっきりと、「平行な辺が1組だけある四角形」を台形としているのである。
その後、6年生の教科書では、次のようなベン図がかかれている。
日本との違いにお気づきだろうか。
ベン図においても、確かに台形と平行四辺形を別の集合に分けているのである。
まさに首尾一貫。
この点に関しては、アメリカの教科書は良く考えられていることが分かる。
このことからも分かるように、日本では
論理的におかしくても、分かりやすければOK
という風潮が、誰もはっきりとは言わないが、あるのではないだろうか。
日本は海外と比べて、論理が軽視されていると言われている。
海外の大学院入試では、よく論理問題が出題されるのに、日本では論理問題を出すところはほとんど無いと言う。
「なかま分け」
というものがある。
つまり、ある観点からいくつかの図形を「なかま分け」するのである。
平行四辺形と台形の学習においても、多くの教科書が「なかま分け」を取り入れている。
では、実際にどのような流れで学習が進められるか見ていこう。
(著作権の関係で問題があるかもしれないので、教科書の画像をそのまま載せることは避けるが、流れは全く同じである)
○日本の教科書の場合
1.まず、いくつかの図形をから、同じなかまに分けるところから始まる。平行な辺の組がいくつあるかで、まず図形を弁別する。

2.台形と平行四辺形の定義をする。
「向かい合う1組の辺が平行な四角形を、台形といいます」
「向かい合う2組の辺が平行な四角形を、平行四辺形といいます」
このように、多くの教科書では台形と平行四辺形を弁別することにより、同時に台形と平行四辺形を学習することになっている。
小学生にとっては、確かに、平行四辺形と台形は全く別の図形であると認識した方が、分かりやすいといえば分かりやすいのである。きわめつけで、例えば『教育出版 小学算数4年下』では、次のような問題できちんと理解しているか、確かめるようになっている。
3.次の図形から、台形と平行四辺形を選びましょう。

(色分けしているが、特に意味はない)
なかま分けで学習が進んできたため、多くの児童は、
台形・・・ウ,エ
平行四辺形・・・ア
というように考える。
教師用の答えの載っている教科書(通称、朱書き教科書)にも、実際上のような解答になっている。
しかし、ここで問題が生じる。
これは、実際にあったことなのだが、ある児童が、
「平行四辺形(ア)も台形じゃないんですか?」
と、質問したのである。
すると先生はなんと答えたかというと、
「アは平行四辺形なんだから、台形じゃないよ」
である。
その質問をした子は、「平行四辺形だって1組は平行な辺があるんだから、台形のなかまじゃないか」と考えて質問したのに対し、なんともトンチンカンな回答を先生がしてしまっていたのだ。
それでも、その子は引き下がらずに、
「平行四辺形だって1組は平行だから・・・」
と続けたのに対し、先生は
「1組だけ平行じゃないと、台形っていわないよね」
と、押し切ったのだ。
日本の多くの教科書では、「なかま分け」により平行四辺形と台形を弁別しているため、暗に台形の定義が「向かい合う辺が1組だけ平行な四角形」と認識されるように仕組まれているのである。
それはそれで構わないかと思うのだが、問題は5年生になってから、教科書に次のようなベン図がかかれているのである。

さあ、あの時先生は、「平行四辺形は台形じゃない」と言ったはずなのに、この図はそうなっていないじゃないか!
ここで、教師は手の平を反すしかなくなる。
「実は、平行四辺形も台形のなかまだったんだ」
この問題について、教育出版に直接問い合わせたところ、
「4年生の段階では、平行四辺形は平行四辺形、台形は台形として学習した方が分かりやすいのでこのようになっていますが、5年生になってからは、平行四辺形も台形のなかまとして見る見方があるんだということに気づければ良いのではないかと思います」
といった内容の返事があった。つまり、
分かりやすければ矛盾することになっても仕方がない
ということだろう。
では、4年生の段階で包摂的な見方で「平行四辺形も台形のなかまではないか?」と考えた子の気持ちはどうなってしまうのだろうか?
より発展的な包摂的な考え方をしたのに、ダメだと言われるのである。
こんなことはあってはならないと思うのだが、実際に教育現場ではそのようなことが行われているのである。
○アメリカの教科書の場合
アメリカの小学校で多く使われている『Houghton Mifflin Math』において、台形と平行四辺形は4年生の教科書に、次のように定義されている。なお、日本とは異なり、「なかま分け」は行っていない。
Trapezoid (台形): A trapezoid has only one pair of parallel sides.
Parallelogram (平行四辺形): A parallelogram has opposite sides parallel and of the same length.
ここで、台形の定義で「only」が使われていることに注目したい。
定義の段階ではっきりと、「平行な辺が1組だけある四角形」を台形としているのである。
その後、6年生の教科書では、次のようなベン図がかかれている。

日本との違いにお気づきだろうか。
ベン図においても、確かに台形と平行四辺形を別の集合に分けているのである。
まさに首尾一貫。
この点に関しては、アメリカの教科書は良く考えられていることが分かる。
このことからも分かるように、日本では
論理的におかしくても、分かりやすければOK
という風潮が、誰もはっきりとは言わないが、あるのではないだろうか。
日本は海外と比べて、論理が軽視されていると言われている。
海外の大学院入試では、よく論理問題が出題されるのに、日本では論理問題を出すところはほとんど無いと言う。
平行四辺形と台形の定義と包摂関係 [算数教育の話]
前回、平行四辺形と台形の定義についてお話しました。
台形の定義として、
「向かい合う1組の辺が平行な四角形」
の「1組」という言葉が「1組以上(あるいは、「少なくとも1組」)」という意味なのか、「1組だけ」なのかで、平行四辺形も台形とするかどうかが決まり、どちらで定義しても構わないが、一貫性が大切だということでした。
(ちなみに、この定義を「1組だけ平行」と捉えるならば、平行四辺形だけではなく「ひし形」や「長方形」、「正方形」も台形ではないということになります。)
一貫性というのは、つまり、「平行四辺形は台形ではない」という立場を取るのであれば、その後もずっと、その立場を崩してはならないということです。
ある時には
「平行四辺形は台形ではありません」
と言っておきながら、また別の時には、
「実は平行四辺形も台形でした」
などと立場を変えられては、とてもじゃありませんが論理的とは言えないでしょう。
実は、このような非論理的なことが、小学校の算数指導において日常的に行われているのです。
なぜ日常的に行われているかというと、
現在の算数の教科書がそのように作られているからです。
教える側の教師も、多少算数や数学に詳しい方であれば、「何かがおかしい」と気づくはずです。
気づいていても、「教科書にそう書いてあるから、まあいいんだろう」と軽く考えている。
教科書会社も、そんな矛盾点があることにも気づかずに、「まあ、そういうものなんだろう」程度に捉えており、一向に改定する気配がありません。
なぜこのような事になっているのかと言うと、算数を教える上で、
「分かりやすさ」
「指導しやすさ」
を優先に考えることに、そのような矛盾も軽く見てしまう原因があるのではないかと思います。
確かに、平行四辺形と台形がどのような四角形かを教える段階では、
「平行四辺形は平行四辺形」
「台形は台形」
と、まったく別物として扱った方が、子どもたちも分かりやすいのです。
つまり、
「この四角形は1組だけ平行な辺があるから台形」
「この四角形は2組とも辺が平行になっているから平行四辺形」
と、まったく区別して教えるのです。
(このことは、2年生に正方形と長方形を教える段階でも同様のことが言えます。)
現在の算数では、台形や平行四辺形について教えても、それらの包摂関係については深入りしないこととなっています。
包摂関係とは、例えば、
「正方形は長方形の仲間である」・・・(正方形)⊂(長方形)
「平行四辺形は台形の仲間である」・・・(平行四辺形)⊂(台形)
のように見る考え方です。
別の分かりやすい例えで言えば、
「人間も生き物の仲間である」
というような見方です。
人間だって生きているんだから、その点では他の生物と同じ仲間ということです。
ですが、多くの教科書や教師は、このような包摂関係を考えるときになって、
「実は平行四辺形も台形と見ることができます」
などと、手の平を反すことになるのです。
では、
教えやすければ、矛盾しようが都合の良いように定義をねじ曲げても良いのか?
ということです。
私個人としては、そのようなご都合主義的な立場で算数を教えてほしくないと思っています。
正直、初めて教科書の中で平気でこのような矛盾が書かれているのを見て、失望にも似た感情を抱きました。
こんな教科書は他の国の教育関係者に見せたら、はっきり言って笑われるだろうなと。
ただただ批判するだけでは意味がないので、では、
本当に日本の教科書ではそうなっているのか?
他の国はどうなんだ?
といったことについて、次回以降またお話できればと思います。
台形の定義として、
「向かい合う1組の辺が平行な四角形」
の「1組」という言葉が「1組以上(あるいは、「少なくとも1組」)」という意味なのか、「1組だけ」なのかで、平行四辺形も台形とするかどうかが決まり、どちらで定義しても構わないが、一貫性が大切だということでした。
(ちなみに、この定義を「1組だけ平行」と捉えるならば、平行四辺形だけではなく「ひし形」や「長方形」、「正方形」も台形ではないということになります。)
一貫性というのは、つまり、「平行四辺形は台形ではない」という立場を取るのであれば、その後もずっと、その立場を崩してはならないということです。
ある時には
「平行四辺形は台形ではありません」
と言っておきながら、また別の時には、
「実は平行四辺形も台形でした」
などと立場を変えられては、とてもじゃありませんが論理的とは言えないでしょう。
実は、このような非論理的なことが、小学校の算数指導において日常的に行われているのです。
なぜ日常的に行われているかというと、
現在の算数の教科書がそのように作られているからです。
教える側の教師も、多少算数や数学に詳しい方であれば、「何かがおかしい」と気づくはずです。
気づいていても、「教科書にそう書いてあるから、まあいいんだろう」と軽く考えている。
教科書会社も、そんな矛盾点があることにも気づかずに、「まあ、そういうものなんだろう」程度に捉えており、一向に改定する気配がありません。
なぜこのような事になっているのかと言うと、算数を教える上で、
「分かりやすさ」
「指導しやすさ」
を優先に考えることに、そのような矛盾も軽く見てしまう原因があるのではないかと思います。
確かに、平行四辺形と台形がどのような四角形かを教える段階では、
「平行四辺形は平行四辺形」
「台形は台形」
と、まったく別物として扱った方が、子どもたちも分かりやすいのです。
つまり、
「この四角形は1組だけ平行な辺があるから台形」
「この四角形は2組とも辺が平行になっているから平行四辺形」
と、まったく区別して教えるのです。
(このことは、2年生に正方形と長方形を教える段階でも同様のことが言えます。)
現在の算数では、台形や平行四辺形について教えても、それらの包摂関係については深入りしないこととなっています。
包摂関係とは、例えば、
「正方形は長方形の仲間である」・・・(正方形)⊂(長方形)
「平行四辺形は台形の仲間である」・・・(平行四辺形)⊂(台形)
のように見る考え方です。
別の分かりやすい例えで言えば、
「人間も生き物の仲間である」
というような見方です。
人間だって生きているんだから、その点では他の生物と同じ仲間ということです。
ですが、多くの教科書や教師は、このような包摂関係を考えるときになって、
「実は平行四辺形も台形と見ることができます」
などと、手の平を反すことになるのです。
では、
教えやすければ、矛盾しようが都合の良いように定義をねじ曲げても良いのか?
ということです。
私個人としては、そのようなご都合主義的な立場で算数を教えてほしくないと思っています。
正直、初めて教科書の中で平気でこのような矛盾が書かれているのを見て、失望にも似た感情を抱きました。
こんな教科書は他の国の教育関係者に見せたら、はっきり言って笑われるだろうなと。
ただただ批判するだけでは意味がないので、では、
本当に日本の教科書ではそうなっているのか?
他の国はどうなんだ?
といったことについて、次回以降またお話できればと思います。
平行四辺形も台形ですか? [算数教育の話]
「平行四辺形も台形ですか?」という問いに対して、ひとつ答えを出すと、
「定義の仕方のよって異なる」
ということです。
平行四辺形の日本の教科書の定義では、
「向かい合う2組の辺が平行な四角形」
というようになっています。
一方、台形は
「向かい合う1組の辺が平行な四角形」
です。
問題は、日本語特有の「あいまいさ」にあります。
この定義の中の「1組」というのは、「1組以上」なのか、「ちょうど1組」という意味なのかがはっきりしていないのです。
なので、人によっては、ちょうど1組なんだから、
「平行四辺形のように2組とも平行になっていたら当てはまらない」
ととる人もいますし、
「平行四辺形だって1組は平行な辺があるんだから当てはまる」
ととる人もいます。
まあ実は、どちらでとっても構わないのですが、重要なことは一貫性です。
数学で重要視されるのは、論理です。
ある時は「AはBだ」といっていたのに、別の時になったら「AはBではない」などと言っていたら、これではとても論理的であるとは言えません。
ひとつの論理体系の中で、矛盾することを述べるのは近代の数学ではあり得ないでしょう。
また、別の機会にこの話について掘り下げたいと思います。
「定義の仕方のよって異なる」
ということです。
平行四辺形の日本の教科書の定義では、
「向かい合う2組の辺が平行な四角形」
というようになっています。
一方、台形は
「向かい合う1組の辺が平行な四角形」
です。
問題は、日本語特有の「あいまいさ」にあります。
この定義の中の「1組」というのは、「1組以上」なのか、「ちょうど1組」という意味なのかがはっきりしていないのです。
なので、人によっては、ちょうど1組なんだから、
「平行四辺形のように2組とも平行になっていたら当てはまらない」
ととる人もいますし、
「平行四辺形だって1組は平行な辺があるんだから当てはまる」
ととる人もいます。
まあ実は、どちらでとっても構わないのですが、重要なことは一貫性です。
数学で重要視されるのは、論理です。
ある時は「AはBだ」といっていたのに、別の時になったら「AはBではない」などと言っていたら、これではとても論理的であるとは言えません。
ひとつの論理体系の中で、矛盾することを述べるのは近代の数学ではあり得ないでしょう。
また、別の機会にこの話について掘り下げたいと思います。



