悪魔の証明の乱用？【リーガルＶ痴漢冤罪事件】 [数学研究室【一般向け】]
最近ドラマなどで「悪魔の証明」という言葉が，多くとは言わないまでも，たまに耳する程度に聞くようになりました。
悪魔の証明とは，古くは「悪魔が存在しないこと」を証明することは不可能だと言われたことが始まりです。
悪魔が存在しないことをどうやって証明したらよいか考えてみてください。
悪魔を実際に見たという人がいなかったとしても，それだけで悪魔が存在しないことの証明にはならないのです。
悪魔は本当はいるのに，単に見つかっていないだけという可能性もあるわけですからね。
つまり「存在する」ということを証明するよりも，「存在しない」ことを証明する方がはるかに困難であるということです。
存在することの証明は，実際に見つければそれで終わりですからね。
まあ，悪魔を実際に見つけることも不可能な気はしますが，そうではなく，方法的に「存在すること」の証明は簡単でも，「存在しないこと」の証明はその方法自体が思いつかないという意味で困難だということです。
このような「ない」ことの証明を，「悪魔の証明」と呼ぶようになったわけですが，よくよく考えると「天使の証明」でも良かったのではないでしょうか。
なんとなく「悪魔の証明」というと，いかにも禍々しい印象から，「困難」や「不可能」という言葉が連想されるため，「天使の証明」ではなく「悪魔の証明」の方がしっくりくるのでしょうね。
さて，ドラマ「リーガルＶ」の初回で，痴漢の冤罪事件が扱われていましたが，その中で「悪魔の証明」という言葉が出てきました。
痴漢をしていないことの証明は「悪魔の証明」だそうです。
しかしこれは，若干「悪魔の証明」の乱用な気がしますね。
悪魔の証明とは，「存在しない」ということの証明であって，「していない」ということの証明ではないはずです。
そもそも，痴漢をしていないことを証明することは難しいと言いますが，よくよく考えてみてください。
痴漢をされたことの証明も難しくないですか？？
痴漢をしていない証明が悪魔の証明であるのなら，痴漢をされたことの証明も悪魔の証明です。
どちらも証明することは困難ですからね。
そうではなく，やはり本来の「存在しない」ことの証明を悪魔の証明と呼ぶべきです。
「した」「していない」の証明ではないのです。
よくドラマの裁判で，「痴漢をしていないことを証明できますか？」と聞きますが，「痴漢をされたことを証明できますか？」は聞いたことがありません。
痴漢の被害者は自分が痴漢されたと主張するだけで証拠の提出を求められることはありませんよね。しかし，なぜ加害者（冤罪であっても）の方は痴漢をしていないと主張しても信じてもらえずに証拠を要求されるのでしょう？
もちろんこれは，被害者を擁護するという立場に立ってのことでしょう。
例えば，「家に泥棒が入りました」と警察に届けて，「泥棒に入られた証拠はありますか？」などと聞かれることなんてありませんよね。
一般的に被害者の供述は根拠もなく信じられるものなのです。
ですが，痴漢の冤罪を考えると，一方的に被害者の供述を信じるだけで良いのか，疑問に感じますね。
悪魔の証明とは，古くは「悪魔が存在しないこと」を証明することは不可能だと言われたことが始まりです。
悪魔が存在しないことをどうやって証明したらよいか考えてみてください。
悪魔を実際に見たという人がいなかったとしても，それだけで悪魔が存在しないことの証明にはならないのです。
悪魔は本当はいるのに，単に見つかっていないだけという可能性もあるわけですからね。
つまり「存在する」ということを証明するよりも，「存在しない」ことを証明する方がはるかに困難であるということです。
存在することの証明は，実際に見つければそれで終わりですからね。
まあ，悪魔を実際に見つけることも不可能な気はしますが，そうではなく，方法的に「存在すること」の証明は簡単でも，「存在しないこと」の証明はその方法自体が思いつかないという意味で困難だということです。
このような「ない」ことの証明を，「悪魔の証明」と呼ぶようになったわけですが，よくよく考えると「天使の証明」でも良かったのではないでしょうか。
なんとなく「悪魔の証明」というと，いかにも禍々しい印象から，「困難」や「不可能」という言葉が連想されるため，「天使の証明」ではなく「悪魔の証明」の方がしっくりくるのでしょうね。
さて，ドラマ「リーガルＶ」の初回で，痴漢の冤罪事件が扱われていましたが，その中で「悪魔の証明」という言葉が出てきました。
痴漢をしていないことの証明は「悪魔の証明」だそうです。
しかしこれは，若干「悪魔の証明」の乱用な気がしますね。
悪魔の証明とは，「存在しない」ということの証明であって，「していない」ということの証明ではないはずです。
そもそも，痴漢をしていないことを証明することは難しいと言いますが，よくよく考えてみてください。
痴漢をされたことの証明も難しくないですか？？
痴漢をしていない証明が悪魔の証明であるのなら，痴漢をされたことの証明も悪魔の証明です。
どちらも証明することは困難ですからね。
そうではなく，やはり本来の「存在しない」ことの証明を悪魔の証明と呼ぶべきです。
「した」「していない」の証明ではないのです。
よくドラマの裁判で，「痴漢をしていないことを証明できますか？」と聞きますが，「痴漢をされたことを証明できますか？」は聞いたことがありません。
痴漢の被害者は自分が痴漢されたと主張するだけで証拠の提出を求められることはありませんよね。しかし，なぜ加害者（冤罪であっても）の方は痴漢をしていないと主張しても信じてもらえずに証拠を要求されるのでしょう？
もちろんこれは，被害者を擁護するという立場に立ってのことでしょう。
例えば，「家に泥棒が入りました」と警察に届けて，「泥棒に入られた証拠はありますか？」などと聞かれることなんてありませんよね。
一般的に被害者の供述は根拠もなく信じられるものなのです。
ですが，痴漢の冤罪を考えると，一方的に被害者の供述を信じるだけで良いのか，疑問に感じますね。
線分の長さが変わってしまう！？【極限の不思議】 [数学研究室【一般向け】]
線分の長さは，どんな測り方をしても，伸ばしたりしない限りは同じはずですよね。
例えば，３０ｃｍ定規が，長さを変えていないのに４５ｃｍになってしまった，なんてことはないわけです。
しかし，長さの測り方に極限の考えを導入すると，事態は一転してしまいます。
長さを変えていないはずなのに，測り方によっては異なる長さになってしまうのです。
そんな不思議な現象を下のプリントにしてみましたので，ぜひご覧ください。
例えば，３０ｃｍ定規が，長さを変えていないのに４５ｃｍになってしまった，なんてことはないわけです。
しかし，長さの測り方に極限の考えを導入すると，事態は一転してしまいます。
長さを変えていないはずなのに，測り方によっては異なる長さになってしまうのです。
そんな不思議な現象を下のプリントにしてみましたので，ぜひご覧ください。
30%で当たる占い師と60%で当たる占い師なら，30%の方を選ぶべし！ [数学研究室【一般向け】]
30%で当たる占い師Ａと，
60%で当たる占い師Ｂがいたとします。
あなたは恋人にプロポーズをしようか迷っているとします。
ＡとＢどちらの占い師に占ってもらうべき？
正解は・・・
Ａの占い師に占ってもらうべきです。
なぜかというと，
Ａの占い師は30%で当たるということは，70%はハズレるということです。
Ｂの占い師は60%で当たるということは，40%はハズレるということです。
なので，Ａの占い師が言ったことと反対のことをすれば，70%の信頼度があるということで，一番信頼度としては高くなりますね。
確率の裏をついた，ちょっとしたトンチでした。
60%で当たる占い師Ｂがいたとします。
あなたは恋人にプロポーズをしようか迷っているとします。
ＡとＢどちらの占い師に占ってもらうべき？
正解は・・・
Ａの占い師に占ってもらうべきです。
なぜかというと，
Ａの占い師は30%で当たるということは，70%はハズレるということです。
Ｂの占い師は60%で当たるということは，40%はハズレるということです。
なので，Ａの占い師が言ったことと反対のことをすれば，70%の信頼度があるということで，一番信頼度としては高くなりますね。
確率の裏をついた，ちょっとしたトンチでした。
サーティワンアイスクリームは元々５種類しかアイスがなかった？【都市伝説】 [数学研究室【一般向け】]
サーティワンアイスクリームのアイスは元々５種類しかなかったという都市伝説をご存知でしょうか？
正式にはバスキン・ロビンスという名称の世界最大級のアイスクリームチェーン店で，日本ではサーティワンアイスクリームと呼ばれることが多いのですが，サーティワンとは英語の「31」で、「31種類のアイスクリームがあるため、1か月毎日違うアイスが楽しめます」という意味が込められているということです。（Wikipediaより）
ですが，実はバスキン・ロビンス創業時には５種類のアイスクリームしかなく，そこから現在の３１種類になったという説です。
その説には数学的な裏付けがあります。
５種類のアイスは何でもいいのですが，例えばバニラ，ストロベリー，チョコレート，ミント，抹茶（！？）の５種類だったとしましょう。
ここから味のバリエーションを増やすために，これら５種類のアイスを混ぜていくとどうなるでしょう？
１）１種類のみの場合・・・元々の５種類
２）２種類選んで混ぜる場合・・・選び方は１０通りある
３）３種類選んで混ぜる場合・・・選び方は１０通りある
４）４種類選んで混ぜる場合・・・選び方は５通りある
５）５種類全部混ぜる場合・・・選び方は１通り
※高校数学のコンビネーションによる計算をすると求まる。
さあ，すべて合わせて何通りになりますか？
そう。
５＋１０＋１０＋５＋１＝３１（通り）
の味が楽しめるわけです。
あるいはもっと簡単に計算するならば，アイスカップに入れるアイスの選び方として，
バニラを入れるか入れないかで２通り
ストロベリーを入れるか入れないかで２通り
チョコレートを入れるか入れないかで２通り
ミントを入れるか入れないかで２通り
抹茶を入れるかいれないかで２通り
すべてかけ合わせると
２×２×２×２×２＝３２（通り）
あることになりますが，すべて選ばないという選択肢を除くと，３１通りのアイスができることになりますね。
これはもちろん都市伝説です。
全部を混ぜただけのアイスなんて，味の想像ができませんね。
正式にはバスキン・ロビンスという名称の世界最大級のアイスクリームチェーン店で，日本ではサーティワンアイスクリームと呼ばれることが多いのですが，サーティワンとは英語の「31」で、「31種類のアイスクリームがあるため、1か月毎日違うアイスが楽しめます」という意味が込められているということです。（Wikipediaより）
ですが，実はバスキン・ロビンス創業時には５種類のアイスクリームしかなく，そこから現在の３１種類になったという説です。
その説には数学的な裏付けがあります。
５種類のアイスは何でもいいのですが，例えばバニラ，ストロベリー，チョコレート，ミント，抹茶（！？）の５種類だったとしましょう。
ここから味のバリエーションを増やすために，これら５種類のアイスを混ぜていくとどうなるでしょう？
１）１種類のみの場合・・・元々の５種類
２）２種類選んで混ぜる場合・・・選び方は１０通りある
３）３種類選んで混ぜる場合・・・選び方は１０通りある
４）４種類選んで混ぜる場合・・・選び方は５通りある
５）５種類全部混ぜる場合・・・選び方は１通り
※高校数学のコンビネーションによる計算をすると求まる。
さあ，すべて合わせて何通りになりますか？
そう。
５＋１０＋１０＋５＋１＝３１（通り）
の味が楽しめるわけです。
あるいはもっと簡単に計算するならば，アイスカップに入れるアイスの選び方として，
バニラを入れるか入れないかで２通り
ストロベリーを入れるか入れないかで２通り
チョコレートを入れるか入れないかで２通り
ミントを入れるか入れないかで２通り
抹茶を入れるかいれないかで２通り
すべてかけ合わせると
２×２×２×２×２＝３２（通り）
あることになりますが，すべて選ばないという選択肢を除くと，３１通りのアイスができることになりますね。
これはもちろん都市伝説です。
全部を混ぜただけのアイスなんて，味の想像ができませんね。
ルート２が無理数であることの証明に関する疑問と注意点 [数学研究室【一般向け】]
２の平方根であるルート２が無理数であることは高校数学で証明法を学びますが，以前から１点ひっかかる点がありました。
背理法による証明が有名だと思いますが，その証明の中で次のような説明を目にすると思います。
「q^2は２の倍数。よってqも２の倍数。」
※q^2はqの２乗の意味
これは，教科書などに載っている証明でもこのように書かれているのですが，次のサイトから引用しました：
https://mathtrain.jp/sqrt2irrational
私が高校生の時，この証明を見て
えっ，なんでqも２の倍数なの？？
と思ったことを今でも覚えているのですが，みなさんも疑問に思ったことはないでしょうか？
さらっと「よってqも２の倍数」と説明もなく書かれていますが，実はこの部分にこそ，ルート２が無理数であることを示す重要なカギが隠れているんです。
少し考えてみましょう。
「q^2は２の倍数。よってqも２の倍数。」・・・（Ａ）
では，
「q^2は４の倍数。よってqも４の倍数。」・・・（Ｂ）
も成り立つのでしょうか？
答えはもちろんＮＯです。
似たような推論なのに，（Ａ）は成り立ちますが，（Ｂ）は成り立たないんです。
もし仮に（Ｂ）が成り立てば，ルート２が無理数であることと全く同じ証明で，ルート４が無理数であることを示せることになってしまいます。
もちろんルート４は２ですから，そんなことがあってはおかしいのです。
ではなぜ（Ａ）が成り立つのかというと，２が素数だからなんです。
（Ａ）の推論の中に隠されていたカギを付け足して書き直すと，
「q^2は２の倍数。２は素数なので，qも２の倍数でなくてはならない。」・・・（Ａ'）
ということなんです。
２が素数だからこの推論は正しくて，逆に４は素数ではないから（Ｂ）は正しくない。
だからルート４に対してはこの証明法は使えないんです。
では，なぜ（Ａ）が成り立つのかというと，
q^2 が2の倍数ということは，
q×q が2でわり切れるということですが，
２は素数なので，q自体が2で割り切れる数でなくてはならないからなのです。
（これは，実はユークリッドの補題の特殊な場合になっています。）
別の言い方をすれば，qを素因数分解したときに2が素因数になければ，q×qを素因数分解しても2は現れないことになってしまうから，q×qが2を素因数としてもつなら，q自体も2を素因数として持っていなければならないということです。
一方，素数ではない４の場合はこの理屈は通用しません。
なぜなら，
q×q が４でわり切れたとしても，qは２で割り切れる数であれば十分だからです。
実際，q=6 だったとすると，qは４でわり切れませんが，q×q=36 は４で割り切れる数になっていますね。
この隠されたカギを理解しておかないと，本当の意味でルート２が無理数であることを理解できたことにはならないのではないでしょうか。
注）q×q が２の倍数ということは，q×q が偶数ということです。
偶数×偶数＝偶数，奇数×奇数＝奇数
なのでq は偶数でなくてはならない，と理解することもできますが，本質はやはり２が素数だからという点でしょう。その本質を理解することで，２だけではなく，他の素数の平方根が無理数であることも同様に証明できることになるのです。
背理法による証明が有名だと思いますが，その証明の中で次のような説明を目にすると思います。
「q^2は２の倍数。よってqも２の倍数。」
※q^2はqの２乗の意味
これは，教科書などに載っている証明でもこのように書かれているのですが，次のサイトから引用しました：
https://mathtrain.jp/sqrt2irrational
私が高校生の時，この証明を見て
えっ，なんでqも２の倍数なの？？
と思ったことを今でも覚えているのですが，みなさんも疑問に思ったことはないでしょうか？
さらっと「よってqも２の倍数」と説明もなく書かれていますが，実はこの部分にこそ，ルート２が無理数であることを示す重要なカギが隠れているんです。
少し考えてみましょう。
「q^2は２の倍数。よってqも２の倍数。」・・・（Ａ）
では，
「q^2は４の倍数。よってqも４の倍数。」・・・（Ｂ）
も成り立つのでしょうか？
答えはもちろんＮＯです。
似たような推論なのに，（Ａ）は成り立ちますが，（Ｂ）は成り立たないんです。
もし仮に（Ｂ）が成り立てば，ルート２が無理数であることと全く同じ証明で，ルート４が無理数であることを示せることになってしまいます。
もちろんルート４は２ですから，そんなことがあってはおかしいのです。
ではなぜ（Ａ）が成り立つのかというと，２が素数だからなんです。
（Ａ）の推論の中に隠されていたカギを付け足して書き直すと，
「q^2は２の倍数。２は素数なので，qも２の倍数でなくてはならない。」・・・（Ａ'）
ということなんです。
２が素数だからこの推論は正しくて，逆に４は素数ではないから（Ｂ）は正しくない。
だからルート４に対してはこの証明法は使えないんです。
では，なぜ（Ａ）が成り立つのかというと，
q^2 が2の倍数ということは，
q×q が2でわり切れるということですが，
２は素数なので，q自体が2で割り切れる数でなくてはならないからなのです。
（これは，実はユークリッドの補題の特殊な場合になっています。）
別の言い方をすれば，qを素因数分解したときに2が素因数になければ，q×qを素因数分解しても2は現れないことになってしまうから，q×qが2を素因数としてもつなら，q自体も2を素因数として持っていなければならないということです。
一方，素数ではない４の場合はこの理屈は通用しません。
なぜなら，
q×q が４でわり切れたとしても，qは２で割り切れる数であれば十分だからです。
実際，q=6 だったとすると，qは４でわり切れませんが，q×q=36 は４で割り切れる数になっていますね。
この隠されたカギを理解しておかないと，本当の意味でルート２が無理数であることを理解できたことにはならないのではないでしょうか。
注）q×q が２の倍数ということは，q×q が偶数ということです。
偶数×偶数＝偶数，奇数×奇数＝奇数
なのでq は偶数でなくてはならない，と理解することもできますが，本質はやはり２が素数だからという点でしょう。その本質を理解することで，２だけではなく，他の素数の平方根が無理数であることも同様に証明できることになるのです。
無理数は有理数よりも遥かに多い？【カントルの対角線論法】 [数学研究室【一般向け】]
これまで集合論に関して，なるべく分かりやすく記事を書いてきましたが，今回はひとつの区切りというかゴールになるのではないかと思います。
つまり，無理数は有理数よりももっと多く存在しているという事についてです。
この事は，1874年にカントルよって区間縮小法に基づく背理法で証明されたのですが，後に有名な対角線論法により，自身で改めて証明をし直したそうです。
数直線上の点はすべてある実数を表しています。
実数は分数で表すことのできる有理数と，分数で表すことのできない無理数とでできています。
数直線は有理数の点でびっしりと埋め尽くされているのですが，それにも関わらず，無理数は有理数よりももっと高い濃度で数直線上に存在しているのです。
数直線は有理数の点と無理数の点の集まりでできています。そもそも不可能な話ですが，例えば０から１の間の数直線を，有理数の点と無理数の点に分けることができたとしましょう。有理数の点だけでも無限にあるのですが，実は無理数の点はそれ以上に多く存在しているということです。
このことは，無限にも階級（ランク）のようなものがあるという事を示しています。
簡単に言えば，順番を付けて並べることができるような無限を「可算無限」，順番を付けて並べることができない無限を「非可算無限」と言い，有理数点は可算無限であるのに対し，無理数点は非可算無限であるということです。可算無限は例えば偶数全体のように，１つひとつの元に順番をつけて無限に並べることができますが，非可算無限はまるで液体のように，１粒１粒並べたとしても，粒がさらに細かく分かれて並べることが出来ないようなものなのです。
記事ですべてを書くことは大変でしたので，プリントにしましたが，なるべく分かりやすく書いたつもりですので，ぜひご一読いただいて，無限の不思議を少しでも読者の皆さまと共有できたらと思います。
無理数の濃度(Page 1)
無理数の濃度(Page 2)
※本記事から初めて読むと難しと思いますので，以下の関連記事を上から順に読んでいただけると，より内容が理解できるかなと思います。
＜YouTubeチャンネル＞
＜関連記事＞
⇒偶数と整数は同じ個数？
⇒有理数と整数は同じ個数？
⇒整数を無限小数で表す【無限小数展開】
⇒実数全体も０から１の間の実数も濃度は一緒？
つまり，無理数は有理数よりももっと多く存在しているという事についてです。
この事は，1874年にカントルよって区間縮小法に基づく背理法で証明されたのですが，後に有名な対角線論法により，自身で改めて証明をし直したそうです。
数直線上の点はすべてある実数を表しています。
実数は分数で表すことのできる有理数と，分数で表すことのできない無理数とでできています。
数直線は有理数の点でびっしりと埋め尽くされているのですが，それにも関わらず，無理数は有理数よりももっと高い濃度で数直線上に存在しているのです。
数直線は有理数の点と無理数の点の集まりでできています。そもそも不可能な話ですが，例えば０から１の間の数直線を，有理数の点と無理数の点に分けることができたとしましょう。有理数の点だけでも無限にあるのですが，実は無理数の点はそれ以上に多く存在しているということです。
このことは，無限にも階級（ランク）のようなものがあるという事を示しています。
簡単に言えば，順番を付けて並べることができるような無限を「可算無限」，順番を付けて並べることができない無限を「非可算無限」と言い，有理数点は可算無限であるのに対し，無理数点は非可算無限であるということです。可算無限は例えば偶数全体のように，１つひとつの元に順番をつけて無限に並べることができますが，非可算無限はまるで液体のように，１粒１粒並べたとしても，粒がさらに細かく分かれて並べることが出来ないようなものなのです。
記事ですべてを書くことは大変でしたので，プリントにしましたが，なるべく分かりやすく書いたつもりですので，ぜひご一読いただいて，無限の不思議を少しでも読者の皆さまと共有できたらと思います。
無理数の濃度(Page 1)
無理数の濃度(Page 2)
※本記事から初めて読むと難しと思いますので，以下の関連記事を上から順に読んでいただけると，より内容が理解できるかなと思います。
＜YouTubeチャンネル＞
＜関連記事＞
⇒偶数と整数は同じ個数？
⇒有理数と整数は同じ個数？
⇒整数を無限小数で表す【無限小数展開】
⇒実数全体も０から１の間の実数も濃度は一緒？
タグ：無限
実数全体も０から１の間の実数も濃度は一緒？【数の不思議】 [数学研究室【一般向け】]
実数の濃度に関して，非常に面白い事実があります。
0 < x < 1 を満たす実数 x の範囲を，区間 (0,1) と表します。
さて，区間 (0,1) には一体どれほどの実数が含まれているのでしょうか？
0.1
0.001
0.21647
などなど，区間 (0,1) だけとっても，無数に実数が含まれているわけです。
では，区間 (0,2) と比べてみましょう。
単純に区間が２倍になったので，２倍の量の実数が含まれているような気がしますよね？
ですが，その直観は残念ながら外れているのです。
〇区間(0,1)と区間(0,2)の実数の個数
次の図を見てください。
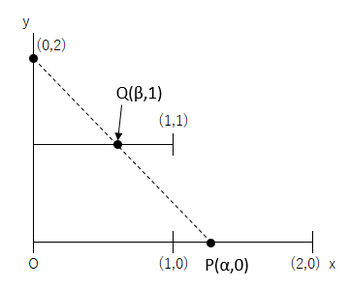
点Pに対して，点Ｑがただ１つ定まります。
点Pの x 座標 α は区間 (0,2) の実数ですが，それに対応して点Ｑの x 座標 β ∈ (0,1)が定まります。
この対応は，区間 (0,2) と区間 (0,1) の１対１対応を与えていますので，区間 (0,1) の実数の個数と区間 (0,2) の実数の個数は等しいということになります。
区間 (0,1) も区間 (0,2) も集合としては無限集合ですので，より正確には２つの集合の濃度は等しいということになります。
〇区間(0,1)の実数と実数全体
さらに不思議なことに，区間 (0,1) に含まれる実数と，数直線全体に含まれる実数全体の濃度ですら，実は等しくなります。
区間 (0,1) の実数と，正の実数 (0,+∞) は次のように１対１に対応させることができます。
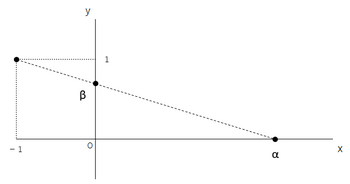
この図のように，xy平面において，任意の実数 α に対してx軸上に点(α,0)をとり，そのと点と点(-1,1)を結ぶ直線をひきます。この直線とy軸との交点を (0,β) とします。
この対応によって，(0,+∞)の実数αに対して(0,1)の実数βが定まります。
逆にβが定まればαもただ１つ定まり，この対応は α∈(0,+∞) とβ∈ (0,1) の１対１対応を与えています。
よって，区間 (0,1) に含まれる実数の濃度と，区間 (0,+∞) に含まれる実数の濃度は等しいということが分かりました。
ここでは簡単に正の実数全体 (0,+∞) と区間 (0,1) の実数を対応させましたが，ここから少し考えれば実数全体 (-∞,+∞) と区間 (0,1) の１対１対応も作ることができます。
無限の世界では，直観では信じられないようなことが起きます。
これは大学１年くらいの集合論の基礎で学びますが，いまだに本当に不思議だと思います。
0 < x < 1 を満たす実数 x の範囲を，区間 (0,1) と表します。
さて，区間 (0,1) には一体どれほどの実数が含まれているのでしょうか？
0.1
0.001
0.21647
などなど，区間 (0,1) だけとっても，無数に実数が含まれているわけです。
では，区間 (0,2) と比べてみましょう。
単純に区間が２倍になったので，２倍の量の実数が含まれているような気がしますよね？
ですが，その直観は残念ながら外れているのです。
〇区間(0,1)と区間(0,2)の実数の個数
次の図を見てください。
点Pに対して，点Ｑがただ１つ定まります。
点Pの x 座標 α は区間 (0,2) の実数ですが，それに対応して点Ｑの x 座標 β ∈ (0,1)が定まります。
この対応は，区間 (0,2) と区間 (0,1) の１対１対応を与えていますので，区間 (0,1) の実数の個数と区間 (0,2) の実数の個数は等しいということになります。
区間 (0,1) も区間 (0,2) も集合としては無限集合ですので，より正確には２つの集合の濃度は等しいということになります。
〇区間(0,1)の実数と実数全体
さらに不思議なことに，区間 (0,1) に含まれる実数と，数直線全体に含まれる実数全体の濃度ですら，実は等しくなります。
区間 (0,1) の実数と，正の実数 (0,+∞) は次のように１対１に対応させることができます。
この図のように，xy平面において，任意の実数 α に対してx軸上に点(α,0)をとり，そのと点と点(-1,1)を結ぶ直線をひきます。この直線とy軸との交点を (0,β) とします。
この対応によって，(0,+∞)の実数αに対して(0,1)の実数βが定まります。
逆にβが定まればαもただ１つ定まり，この対応は α∈(0,+∞) とβ∈ (0,1) の１対１対応を与えています。
よって，区間 (0,1) に含まれる実数の濃度と，区間 (0,+∞) に含まれる実数の濃度は等しいということが分かりました。
ここでは簡単に正の実数全体 (0,+∞) と区間 (0,1) の実数を対応させましたが，ここから少し考えれば実数全体 (-∞,+∞) と区間 (0,1) の１対１対応も作ることができます。
無限の世界では，直観では信じられないようなことが起きます。
これは大学１年くらいの集合論の基礎で学びますが，いまだに本当に不思議だと思います。
タグ：無限
整数を無限小数で表す【無限小数展開】 [数学研究室【一般向け】]
以前の記事で，偶数全体や奇数全体，有理数全体は整数（または自然数）全体と同じ個数（濃度）であることを紹介してきました。
⇒【偶数と整数は同じ個数？】
⇒【有理数と整数は同じ個数？】
そこで，整数や有理数よりももっと多く存在する数として，無理数があることを軽く触れました。
分数で表すことのできる数である有理数は，数直線上びっしりと詰まっているのですが，それよりも高い濃度で無理数は数直線上に敷き詰まっているといったイメージです。
このことを示すのに，無限小数展開を先に紹介した方が都合がよいので，以下プリントにまとめて紹介させていただきます。
また，実数と有理数・無理数の関係もまとめておきましたので，ご覧いただければと思います。
無限小数展開（実数と有理数・無理数）１ページ目
無限小数展開（実数と有理数・無理数）２ページ目
これらを踏まえて，次回以降，無理数が有理数よりももっと高い濃度で数直線上に存在していることをご紹介できればと思います。
＜関連記事＞
⇒【偶数と整数は同じ個数？】
⇒【有理数と整数は同じ個数？】
⇒【無限小数と極限の関係】
⇒【偶数と整数は同じ個数？】
⇒【有理数と整数は同じ個数？】
そこで，整数や有理数よりももっと多く存在する数として，無理数があることを軽く触れました。
分数で表すことのできる数である有理数は，数直線上びっしりと詰まっているのですが，それよりも高い濃度で無理数は数直線上に敷き詰まっているといったイメージです。
このことを示すのに，無限小数展開を先に紹介した方が都合がよいので，以下プリントにまとめて紹介させていただきます。
また，実数と有理数・無理数の関係もまとめておきましたので，ご覧いただければと思います。
無限小数展開（実数と有理数・無理数）１ページ目
無限小数展開（実数と有理数・無理数）２ページ目
これらを踏まえて，次回以降，無理数が有理数よりももっと高い濃度で数直線上に存在していることをご紹介できればと思います。
＜関連記事＞
⇒【偶数と整数は同じ個数？】
⇒【有理数と整数は同じ個数？】
⇒【無限小数と極限の関係】
タグ：無限
一次方程式の解はなぜひとつ？【当たり前を問う】 [数学研究室【一般向け】]
一次方程式は一般に
ax+b=0
という形をしています。
xが未知数，aとbは係数です。
係数は整数でも，実数でも複素数でもなんでもいいのですが，a=0だと一次方程式にはなりませんので，a=0ではないとします。
解は，x=-a/b で求められるのですが，では，
「本当に他に解はないのですか？」
と言ったら，きちんと説明できるでしょうか？
一次方程式なんだから解は１つでしょと思われるでしょうが，
では，一次方程式だとなぜ解は１つなのか？
当たり前のことでも根本に戻って考える事が，さらに発展的な思考に結びつきます。
〇当たり前を問う
例えば，２x＋１＝０の解は，ｘ＝-1/2 ですが，本当に他に解がないことが言えるのかということです。
一般に，解が１つ見つかったところで，それで他に解が存在しないとは言い切れません。
実際，二次方程式になると，x^2＝4 （x^2はxの２乗）の解は，x=2 ですが，他にも解 x=-2 があるわけですよね。
つまり，方程式は一般には，
「解が見つかった」
ということと，
「解が他にはない」
ということは直接的には結びつかないのです。
では改めて，なぜ一次方程式だと解は１つしかないと言えるのか。
そんなに難しいことはありませんので，ぜひ皆さんも考えてみてくださいね。
考え方は様々あると思いますが，一例をプリントにまとめましたので，ご覧いただければと思います。
ax+b=0
という形をしています。
xが未知数，aとbは係数です。
係数は整数でも，実数でも複素数でもなんでもいいのですが，a=0だと一次方程式にはなりませんので，a=0ではないとします。
解は，x=-a/b で求められるのですが，では，
「本当に他に解はないのですか？」
と言ったら，きちんと説明できるでしょうか？
一次方程式なんだから解は１つでしょと思われるでしょうが，
では，一次方程式だとなぜ解は１つなのか？
当たり前のことでも根本に戻って考える事が，さらに発展的な思考に結びつきます。
〇当たり前を問う
例えば，２x＋１＝０の解は，ｘ＝-1/2 ですが，本当に他に解がないことが言えるのかということです。
一般に，解が１つ見つかったところで，それで他に解が存在しないとは言い切れません。
実際，二次方程式になると，x^2＝4 （x^2はxの２乗）の解は，x=2 ですが，他にも解 x=-2 があるわけですよね。
つまり，方程式は一般には，
「解が見つかった」
ということと，
「解が他にはない」
ということは直接的には結びつかないのです。
では改めて，なぜ一次方程式だと解は１つしかないと言えるのか。
そんなに難しいことはありませんので，ぜひ皆さんも考えてみてくださいね。
考え方は様々あると思いますが，一例をプリントにまとめましたので，ご覧いただければと思います。
有理数と整数は同じ個数？【いかにして分数を並べるか】 [数学研究室【一般向け】]
前回，偶数と整数は同じ個数であることをご紹介させていただきました。
⇒【偶数と整数は同じ個数？】
正確には，整数全体と偶数全体の濃度が等しいということなのですが，実は有理数（分数で表すことのできる数）全体の濃度も，整数全体の濃度と等しくなります。
本質的には同じなので，ここでは整数や有理数はすべて正の数のみに限定して話を進めていきます。
〇整数全体と同じ濃度（個数）とは？
整数と同じ濃度であるというのは，１から順番に整数を対応させることができるということです。
なので，偶数であれば，小さい順に
２，４，６，８，１０，１２，・・・
というように並べることができるので，１から順番に整数を対応させることができ，この対応により整数全体と偶数全体は１対１対に対応させることができたのでした。
つまり，整数と同じ濃度であるということは，このように順番をつけて無限に１列に並べることができるということです。
なので，偶数に限らず，３の倍数や５の倍数なども，順番をつけて無限に１列に並べることができるので，整数と同じ濃度を持っています。
〇分数をいかに並べるか
有理数というのは，分数で表すことのできる数です。
偶数や３の倍数などは，小さい順に並べることで自然に１列に並ばせることができるのですが，有理数の場合はそうはいきません。
なぜなら，有理数を小さい順に並べようとしても，最も小さな有理数というのは存在しないからです。
例えば，1/2（２分の１）よりも1/4の方が小さく，さらに1/4よりも1/8の方が小さくなるように，ある有理数があれば，それを半分の大きさにした数もまた有理数だからです。
いくらでも小さな有理数が作れてしまうのですから，有理数を小さい順に並べること自体不可能なのです。
では，どのように有理数を１列に並べるかというと，次のようにします。
1/1 2/1 3/1 4/1 5/1 6/1 ・・・
1/2 2/2 3/2 4/2 5/2 6/2 ・・・
1/3 2/3 3/3 4/3 5/3 6/3 ・・・
1/4 2/4 3/4 4/4 5/4 6/4 ・・・
1/5 2/5 3/5 4/5 5/5 6/5 ・・・
・・・・・・・・・・・・・・
上から１行目には分母が１の分数を，
上から２行目には分母が２の分数を，
上から３行目には分母が３の分数を，
それぞれ小さい順に並べることができますね。
この並びにより，有理数全体を平面上に並べることができます。
では，この並びに対して，整数を次のように割り当てていきます。
1 2 6 7 ・・・
3 5 8 ・・・
4 9 ・・・
10 ・・・
・・・
つまり，左上の1/1からスタートして，この分数を斜めに数えていくということです。
このように分数に順序をつけることで，１番目から順に分数を余すことなく１列に並べることができるのです。
もちろん，約分することで同じ分数になってしまうこともありますが，約分して同じになる分数が出てくれば，それはとばして並べていくことで，重複なく１列に並べることができます。
この並びにより，整数全体と有理数全体は１対１に対応させることができるので，有理数全体と整数全体は同じ濃度であると言えるのです。
このように有理数全体ですら，余すことなくきれいに１列に整列させることができるのですから，もう何でも整数全体と同じ濃度なのではないかと思ってしまいますが，実はより高い濃度の無限集合があるのです。
その集合こそ，無理数全体の集合なのですが，この話はまた次回以降にしたいと思います。
追記：分数の並びが見づらいと思いましたので，プリントにして少し見やすくしました。
＊YouTubeチャンネル＊
＜関連記事＞
⇒【偶数と整数は同じ個数？】
⇒【偶数と整数は同じ個数？】
正確には，整数全体と偶数全体の濃度が等しいということなのですが，実は有理数（分数で表すことのできる数）全体の濃度も，整数全体の濃度と等しくなります。
本質的には同じなので，ここでは整数や有理数はすべて正の数のみに限定して話を進めていきます。
〇整数全体と同じ濃度（個数）とは？
整数と同じ濃度であるというのは，１から順番に整数を対応させることができるということです。
なので，偶数であれば，小さい順に
２，４，６，８，１０，１２，・・・
というように並べることができるので，１から順番に整数を対応させることができ，この対応により整数全体と偶数全体は１対１対に対応させることができたのでした。
つまり，整数と同じ濃度であるということは，このように順番をつけて無限に１列に並べることができるということです。
なので，偶数に限らず，３の倍数や５の倍数なども，順番をつけて無限に１列に並べることができるので，整数と同じ濃度を持っています。
〇分数をいかに並べるか
有理数というのは，分数で表すことのできる数です。
偶数や３の倍数などは，小さい順に並べることで自然に１列に並ばせることができるのですが，有理数の場合はそうはいきません。
なぜなら，有理数を小さい順に並べようとしても，最も小さな有理数というのは存在しないからです。
例えば，1/2（２分の１）よりも1/4の方が小さく，さらに1/4よりも1/8の方が小さくなるように，ある有理数があれば，それを半分の大きさにした数もまた有理数だからです。
いくらでも小さな有理数が作れてしまうのですから，有理数を小さい順に並べること自体不可能なのです。
では，どのように有理数を１列に並べるかというと，次のようにします。
1/1 2/1 3/1 4/1 5/1 6/1 ・・・
1/2 2/2 3/2 4/2 5/2 6/2 ・・・
1/3 2/3 3/3 4/3 5/3 6/3 ・・・
1/4 2/4 3/4 4/4 5/4 6/4 ・・・
1/5 2/5 3/5 4/5 5/5 6/5 ・・・
・・・・・・・・・・・・・・
上から１行目には分母が１の分数を，
上から２行目には分母が２の分数を，
上から３行目には分母が３の分数を，
それぞれ小さい順に並べることができますね。
この並びにより，有理数全体を平面上に並べることができます。
では，この並びに対して，整数を次のように割り当てていきます。
1 2 6 7 ・・・
3 5 8 ・・・
4 9 ・・・
10 ・・・
・・・
つまり，左上の1/1からスタートして，この分数を斜めに数えていくということです。
このように分数に順序をつけることで，１番目から順に分数を余すことなく１列に並べることができるのです。
もちろん，約分することで同じ分数になってしまうこともありますが，約分して同じになる分数が出てくれば，それはとばして並べていくことで，重複なく１列に並べることができます。
この並びにより，整数全体と有理数全体は１対１に対応させることができるので，有理数全体と整数全体は同じ濃度であると言えるのです。
このように有理数全体ですら，余すことなくきれいに１列に整列させることができるのですから，もう何でも整数全体と同じ濃度なのではないかと思ってしまいますが，実はより高い濃度の無限集合があるのです。
その集合こそ，無理数全体の集合なのですが，この話はまた次回以降にしたいと思います。
追記：分数の並びが見づらいと思いましたので，プリントにして少し見やすくしました。
＊YouTubeチャンネル＊
＜関連記事＞
⇒【偶数と整数は同じ個数？】
