教員の残業について話そうか【働き方改革？何それおいしいの？】 [その他の話]
働き方改革の実施が叫ばれている昨今，教育の現場ではどうなっているか話をしましょう。
世間の一部の企業では，１９時には完全に電気を切って全員退社するように促すなど，積極的な試みがなされていますが，教育の現場では，はっきり言って何も変わっていません。
教員の残業代というのは，公立や私学での違いなどはあるとは思いますが，概ね「みなし残業」となっています。
つまり，基本給の何パーセントかが，あらかじめ手当として上乗せされているのです。
なので，毎日定時で帰ったとしても残業をしたとみなされ，手当が支給されます。
なんだ，残業しなくても手当がつくならいいじゃん
と思うかもしれませんが，実態はそうなっていません。
つまり，いくら残業をしたとしても一定の残業手当しか支給されないということです。
例えば，１５時間分の残業代が「みなし残業手当」として上乗せされていたとしても，実態は６０時間残業しようと，１００時間残業しようと，１５時間分の残業手当しか支給されないのです。
そんなの，実際の残業時間を学校側が把握していればその分を上乗せすればいいじゃないかと思うかもしれませんが，実際の残業時間なんて，ほぼ誰も把握していないんです。
みなし残業以上の残業をしたと言っても，上はそれを認めずもみ消しているのが実態です。
何せ実際の残業時間を把握していないのですから。
タイムカードがあるところもあると思いますが，実はタイムカードを学校に出るときに打刻したとしても，その時間がそのまま残業時間に反映されるわけではないのです。
教員という職業の特殊性もあるのかもしれませんが，教材研究などはやり出せばキリがありません。
だらだらと長時間，教材研究という名目で学校に居座る教員もいますからね。
もちろん真面目に教材研究や授業準備などで居残る教員も多くいますが，学校にいた時間の内，いったいどれだけの時間を残業として認めればよいのかの判断が付きにくいのです。
教育の現場でも，確かに働き方改革の一環で残業時間の縮減が求められているのです。
しかしこのように，学校に教員がいる時間の内，どれだけの時間が実質的な勤務時間になるのか判断が付きにくいという性質から，実際にはかなり多くの残業をしているにも関わらず，「記録としての残業時間」を減らすことで，あたかも残業時間が減ったかのように見せかけているだけなのです。
実質的には，最近何かと問題視されている定量裁量制と何ら変わらないことになっているのですね。
アベノミクスで世間では給料が僅かながらにでも上がったという話も聞きますが，それすら教員には無関係です。
ボーナスが上がった？
いつもと変わりません。
残業時間？
前と変わりません。
そんなのが，教員の仕事の実態です。
もちろん私学や一部の地域では「真面目に」働き方改革に取り組んでいる学校もあると思いますが，まだまだそう多くはないと思います。
世間の一部の企業では，１９時には完全に電気を切って全員退社するように促すなど，積極的な試みがなされていますが，教育の現場では，はっきり言って何も変わっていません。
教員の残業代というのは，公立や私学での違いなどはあるとは思いますが，概ね「みなし残業」となっています。
つまり，基本給の何パーセントかが，あらかじめ手当として上乗せされているのです。
なので，毎日定時で帰ったとしても残業をしたとみなされ，手当が支給されます。
なんだ，残業しなくても手当がつくならいいじゃん
と思うかもしれませんが，実態はそうなっていません。
つまり，いくら残業をしたとしても一定の残業手当しか支給されないということです。
例えば，１５時間分の残業代が「みなし残業手当」として上乗せされていたとしても，実態は６０時間残業しようと，１００時間残業しようと，１５時間分の残業手当しか支給されないのです。
そんなの，実際の残業時間を学校側が把握していればその分を上乗せすればいいじゃないかと思うかもしれませんが，実際の残業時間なんて，ほぼ誰も把握していないんです。
みなし残業以上の残業をしたと言っても，上はそれを認めずもみ消しているのが実態です。
何せ実際の残業時間を把握していないのですから。
タイムカードがあるところもあると思いますが，実はタイムカードを学校に出るときに打刻したとしても，その時間がそのまま残業時間に反映されるわけではないのです。
教員という職業の特殊性もあるのかもしれませんが，教材研究などはやり出せばキリがありません。
だらだらと長時間，教材研究という名目で学校に居座る教員もいますからね。
もちろん真面目に教材研究や授業準備などで居残る教員も多くいますが，学校にいた時間の内，いったいどれだけの時間を残業として認めればよいのかの判断が付きにくいのです。
教育の現場でも，確かに働き方改革の一環で残業時間の縮減が求められているのです。
しかしこのように，学校に教員がいる時間の内，どれだけの時間が実質的な勤務時間になるのか判断が付きにくいという性質から，実際にはかなり多くの残業をしているにも関わらず，「記録としての残業時間」を減らすことで，あたかも残業時間が減ったかのように見せかけているだけなのです。
実質的には，最近何かと問題視されている定量裁量制と何ら変わらないことになっているのですね。
アベノミクスで世間では給料が僅かながらにでも上がったという話も聞きますが，それすら教員には無関係です。
ボーナスが上がった？
いつもと変わりません。
残業時間？
前と変わりません。
そんなのが，教員の仕事の実態です。
もちろん私学や一部の地域では「真面目に」働き方改革に取り組んでいる学校もあると思いますが，まだまだそう多くはないと思います。
30%で当たる占い師と60%で当たる占い師なら，30%の方を選ぶべし！ [数学研究室【一般向け】]
30%で当たる占い師Ａと，
60%で当たる占い師Ｂがいたとします。
あなたは恋人にプロポーズをしようか迷っているとします。
ＡとＢどちらの占い師に占ってもらうべき？
正解は・・・
Ａの占い師に占ってもらうべきです。
なぜかというと，
Ａの占い師は30%で当たるということは，70%はハズレるということです。
Ｂの占い師は60%で当たるということは，40%はハズレるということです。
なので，Ａの占い師が言ったことと反対のことをすれば，70%の信頼度があるということで，一番信頼度としては高くなりますね。
確率の裏をついた，ちょっとしたトンチでした。
60%で当たる占い師Ｂがいたとします。
あなたは恋人にプロポーズをしようか迷っているとします。
ＡとＢどちらの占い師に占ってもらうべき？
正解は・・・
Ａの占い師に占ってもらうべきです。
なぜかというと，
Ａの占い師は30%で当たるということは，70%はハズレるということです。
Ｂの占い師は60%で当たるということは，40%はハズレるということです。
なので，Ａの占い師が言ったことと反対のことをすれば，70%の信頼度があるということで，一番信頼度としては高くなりますね。
確率の裏をついた，ちょっとしたトンチでした。
等積変形の利用【ハイレベル算数】（解説編） [算数研究室【小学生向け】]
前回出題した問題の解説をアップしました。
次のような問題でしたね。
（問題編）
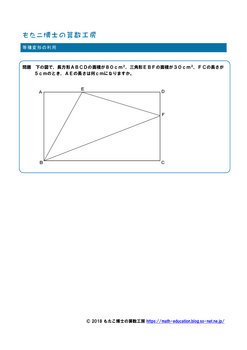
この長方形の中の三角形をいかにうまく等積変形するか，ほぼヒラメキに頼るしかなさそうな感じですが，１度理解すると似たような問題が出た時にも，考え方を活かせると思います。
解説編は下のプリントですので，ご覧いただければと思います。
また，何か別の解法があれば，教えていただければと思います。
（解説編）
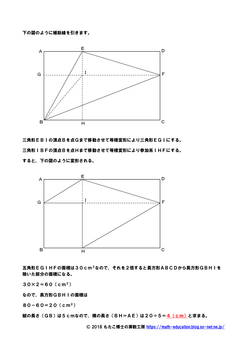
このように長方形の中に三角形がある場合には，別の等積変形の仕方もありますので，補足として下のプリントに載せておきます。しかし，この問題の場合には，うまく適用することができませんが，もしかすると，この等積変形の方法でも解くことができるかもしれませんので，解けた場合にはコメント等でお知らせいただければと思います。
（補足プリント）
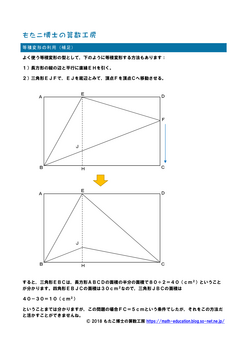
次のような問題でしたね。
（問題編）
この長方形の中の三角形をいかにうまく等積変形するか，ほぼヒラメキに頼るしかなさそうな感じですが，１度理解すると似たような問題が出た時にも，考え方を活かせると思います。
解説編は下のプリントですので，ご覧いただければと思います。
また，何か別の解法があれば，教えていただければと思います。
（解説編）
このように長方形の中に三角形がある場合には，別の等積変形の仕方もありますので，補足として下のプリントに載せておきます。しかし，この問題の場合には，うまく適用することができませんが，もしかすると，この等積変形の方法でも解くことができるかもしれませんので，解けた場合にはコメント等でお知らせいただければと思います。
（補足プリント）
等積変形の利用【ハイレベル算数】 [算数研究室【小学生向け】]
三角形の等積変形を利用する問題は多数ありますが，この問題はかなりハイレベルな見方が必要です。
一見簡単そうな形なのですが，うまく等積変形をしないと解くことはできません。
私も初めて見た時には，なかなか手も足も出なかった記憶があります。
中学の入試問題でもたまに見かける形ですが，一度どのように等積変形したら良いかを理解しておくと，似たような問題にも適用できるのではないかと思います。
ぜひ一度じっくりと考えてみてくださいね！
解説は後日アップします。
一見簡単そうな形なのですが，うまく等積変形をしないと解くことはできません。
私も初めて見た時には，なかなか手も足も出なかった記憶があります。
中学の入試問題でもたまに見かける形ですが，一度どのように等積変形したら良いかを理解しておくと，似たような問題にも適用できるのではないかと思います。
ぜひ一度じっくりと考えてみてくださいね！
解説は後日アップします。
０で割ることはなぜできない？【１÷０】 [算数研究室【小学生向け】]
わり算では０で割ることは考えないことになっていますね。
考えないというより，答えが求まらないという方が正確かもしれません。
例えば，１÷０を考えてみます。
わり算というのはその意味のひとつに
「１の中に０が何個入るか」
を求めることがあります。
つまり，
０×□＝１
をみたす□を求めることが，１÷０の計算です。
しかし，０に何をかけても０なので，１になることはないのですね。
しかし，解として
１÷０＝∞
という話をたまに聞きます。
これは，次のように，わる数をどんどん小さくしていくと，答えがどんどん大きくなり，答えは無限大になるということですね。
１÷０.１＝１０
１÷０.０１＝１００
１÷０.００１＝１０００
これは割る数を０に近づけていくという，一種の極限なのですが，ではマイナスの方から０に近づけたらどうなるでしょう？（中学の数学の知識が必要です）
１÷（－０.１）＝－１０
１÷（－０.０１）＝－１００
１÷（－０.００１）＝－１０００
となり，形式的には
１÷０＝－∞
となってしまいますね。
やはり答えが+∞か，-∞かで定まりません。
しかしそもそも，∞という数はないのです。
１÷ｘのｘを正の方から０に近づけると+∞に発散し，
１÷ｘのｘを負の方から０に近づけると-∞に発散する
という，いくらでも大きくなってしまい定まった値に近づかない（ある値に近づくことを収束，それ以外を発散するといいます）ことを表しているんですね。
〇０を０で割る場合
０÷０の場合は若干特殊です。
０×□＝０
で□に当てはまる数が答えですが，□には何を当てはめてもこの式は成り立ってしまいます。
ですので，これも答えが定まらないことになってしまいますね。
なので，やはり０÷０も意味がないので考えないことになっています。
考えないというより，答えが求まらないという方が正確かもしれません。
例えば，１÷０を考えてみます。
わり算というのはその意味のひとつに
「１の中に０が何個入るか」
を求めることがあります。
つまり，
０×□＝１
をみたす□を求めることが，１÷０の計算です。
しかし，０に何をかけても０なので，１になることはないのですね。
しかし，解として
１÷０＝∞
という話をたまに聞きます。
これは，次のように，わる数をどんどん小さくしていくと，答えがどんどん大きくなり，答えは無限大になるということですね。
１÷０.１＝１０
１÷０.０１＝１００
１÷０.００１＝１０００
これは割る数を０に近づけていくという，一種の極限なのですが，ではマイナスの方から０に近づけたらどうなるでしょう？（中学の数学の知識が必要です）
１÷（－０.１）＝－１０
１÷（－０.０１）＝－１００
１÷（－０.００１）＝－１０００
となり，形式的には
１÷０＝－∞
となってしまいますね。
やはり答えが+∞か，-∞かで定まりません。
しかしそもそも，∞という数はないのです。
１÷ｘのｘを正の方から０に近づけると+∞に発散し，
１÷ｘのｘを負の方から０に近づけると-∞に発散する
という，いくらでも大きくなってしまい定まった値に近づかない（ある値に近づくことを収束，それ以外を発散するといいます）ことを表しているんですね。
〇０を０で割る場合
０÷０の場合は若干特殊です。
０×□＝０
で□に当てはまる数が答えですが，□には何を当てはめてもこの式は成り立ってしまいます。
ですので，これも答えが定まらないことになってしまいますね。
なので，やはり０÷０も意味がないので考えないことになっています。
立方体だと思うでしょう？【直観は外れることもある】 [算数研究室【小学生向け】]
下の図のように，１辺が１２ｃｍの正方形の厚紙の四隅（よすみ）を切り取り，直方体の形の容器を作ります。ふたは作りません。
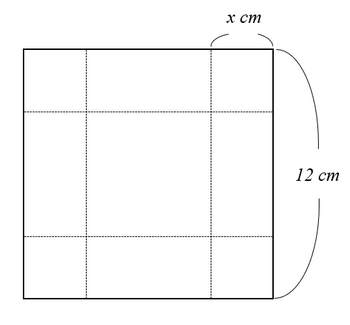
直方体の容積が最も大きくなるのは，図中のxがいくつのときでしょうか？
こういうのは大抵，立方体の時がどうせ最大になるんでしょ？
だから x=4 の時でしょ？
と，思いますよね。
でも，予想に反し，実は立方体のときではないのです。
直観は大切ですが，時に外れることもあるんです。
正解は
x=2
のときです。
つまり，端から６分の１のところの四隅を切り取って直方体を作るときが，最も容積が大きくなるんです。
どうやって調べるのかというと，この容器の容積を x の関数と見れば三次関数になるので，０≦ｘ≦６ の範囲で最大値を調べれば，x=2のときに最大となることが分かるのです。
ではなぜx=2のときなのでしょう？
高校数学の知識があれば，x=2の時が最大だと分かるのですが，「分かること」と「納得すること」は別です。
時に数学的には理解できても，なぜなのか納得できないこともあるのです。
直方体の容積が最も大きくなるのは，図中のxがいくつのときでしょうか？
こういうのは大抵，立方体の時がどうせ最大になるんでしょ？
だから x=4 の時でしょ？
と，思いますよね。
でも，予想に反し，実は立方体のときではないのです。
直観は大切ですが，時に外れることもあるんです。
正解は
x=2
のときです。
つまり，端から６分の１のところの四隅を切り取って直方体を作るときが，最も容積が大きくなるんです。
どうやって調べるのかというと，この容器の容積を x の関数と見れば三次関数になるので，０≦ｘ≦６ の範囲で最大値を調べれば，x=2のときに最大となることが分かるのです。
ではなぜx=2のときなのでしょう？
高校数学の知識があれば，x=2の時が最大だと分かるのですが，「分かること」と「納得すること」は別です。
時に数学的には理解できても，なぜなのか納得できないこともあるのです。
サーティワンアイスクリームは元々５種類しかアイスがなかった？【都市伝説】 [数学研究室【一般向け】]
サーティワンアイスクリームのアイスは元々５種類しかなかったという都市伝説をご存知でしょうか？
正式にはバスキン・ロビンスという名称の世界最大級のアイスクリームチェーン店で，日本ではサーティワンアイスクリームと呼ばれることが多いのですが，サーティワンとは英語の「31」で、「31種類のアイスクリームがあるため、1か月毎日違うアイスが楽しめます」という意味が込められているということです。（Wikipediaより）
ですが，実はバスキン・ロビンス創業時には５種類のアイスクリームしかなく，そこから現在の３１種類になったという説です。
その説には数学的な裏付けがあります。
５種類のアイスは何でもいいのですが，例えばバニラ，ストロベリー，チョコレート，ミント，抹茶（！？）の５種類だったとしましょう。
ここから味のバリエーションを増やすために，これら５種類のアイスを混ぜていくとどうなるでしょう？
１）１種類のみの場合・・・元々の５種類
２）２種類選んで混ぜる場合・・・選び方は１０通りある
３）３種類選んで混ぜる場合・・・選び方は１０通りある
４）４種類選んで混ぜる場合・・・選び方は５通りある
５）５種類全部混ぜる場合・・・選び方は１通り
※高校数学のコンビネーションによる計算をすると求まる。
さあ，すべて合わせて何通りになりますか？
そう。
５＋１０＋１０＋５＋１＝３１（通り）
の味が楽しめるわけです。
あるいはもっと簡単に計算するならば，アイスカップに入れるアイスの選び方として，
バニラを入れるか入れないかで２通り
ストロベリーを入れるか入れないかで２通り
チョコレートを入れるか入れないかで２通り
ミントを入れるか入れないかで２通り
抹茶を入れるかいれないかで２通り
すべてかけ合わせると
２×２×２×２×２＝３２（通り）
あることになりますが，すべて選ばないという選択肢を除くと，３１通りのアイスができることになりますね。
これはもちろん都市伝説です。
全部を混ぜただけのアイスなんて，味の想像ができませんね。
正式にはバスキン・ロビンスという名称の世界最大級のアイスクリームチェーン店で，日本ではサーティワンアイスクリームと呼ばれることが多いのですが，サーティワンとは英語の「31」で、「31種類のアイスクリームがあるため、1か月毎日違うアイスが楽しめます」という意味が込められているということです。（Wikipediaより）
ですが，実はバスキン・ロビンス創業時には５種類のアイスクリームしかなく，そこから現在の３１種類になったという説です。
その説には数学的な裏付けがあります。
５種類のアイスは何でもいいのですが，例えばバニラ，ストロベリー，チョコレート，ミント，抹茶（！？）の５種類だったとしましょう。
ここから味のバリエーションを増やすために，これら５種類のアイスを混ぜていくとどうなるでしょう？
１）１種類のみの場合・・・元々の５種類
２）２種類選んで混ぜる場合・・・選び方は１０通りある
３）３種類選んで混ぜる場合・・・選び方は１０通りある
４）４種類選んで混ぜる場合・・・選び方は５通りある
５）５種類全部混ぜる場合・・・選び方は１通り
※高校数学のコンビネーションによる計算をすると求まる。
さあ，すべて合わせて何通りになりますか？
そう。
５＋１０＋１０＋５＋１＝３１（通り）
の味が楽しめるわけです。
あるいはもっと簡単に計算するならば，アイスカップに入れるアイスの選び方として，
バニラを入れるか入れないかで２通り
ストロベリーを入れるか入れないかで２通り
チョコレートを入れるか入れないかで２通り
ミントを入れるか入れないかで２通り
抹茶を入れるかいれないかで２通り
すべてかけ合わせると
２×２×２×２×２＝３２（通り）
あることになりますが，すべて選ばないという選択肢を除くと，３１通りのアイスができることになりますね。
これはもちろん都市伝説です。
全部を混ぜただけのアイスなんて，味の想像ができませんね。
ルート２が無理数であることの証明に関する疑問と注意点 [数学研究室【一般向け】]
２の平方根であるルート２が無理数であることは高校数学で証明法を学びますが，以前から１点ひっかかる点がありました。
背理法による証明が有名だと思いますが，その証明の中で次のような説明を目にすると思います。
「q^2は２の倍数。よってqも２の倍数。」
※q^2はqの２乗の意味
これは，教科書などに載っている証明でもこのように書かれているのですが，次のサイトから引用しました：
https://mathtrain.jp/sqrt2irrational
私が高校生の時，この証明を見て
えっ，なんでqも２の倍数なの？？
と思ったことを今でも覚えているのですが，みなさんも疑問に思ったことはないでしょうか？
さらっと「よってqも２の倍数」と説明もなく書かれていますが，実はこの部分にこそ，ルート２が無理数であることを示す重要なカギが隠れているんです。
少し考えてみましょう。
「q^2は２の倍数。よってqも２の倍数。」・・・（Ａ）
では，
「q^2は４の倍数。よってqも４の倍数。」・・・（Ｂ）
も成り立つのでしょうか？
答えはもちろんＮＯです。
似たような推論なのに，（Ａ）は成り立ちますが，（Ｂ）は成り立たないんです。
もし仮に（Ｂ）が成り立てば，ルート２が無理数であることと全く同じ証明で，ルート４が無理数であることを示せることになってしまいます。
もちろんルート４は２ですから，そんなことがあってはおかしいのです。
ではなぜ（Ａ）が成り立つのかというと，２が素数だからなんです。
（Ａ）の推論の中に隠されていたカギを付け足して書き直すと，
「q^2は２の倍数。２は素数なので，qも２の倍数でなくてはならない。」・・・（Ａ'）
ということなんです。
２が素数だからこの推論は正しくて，逆に４は素数ではないから（Ｂ）は正しくない。
だからルート４に対してはこの証明法は使えないんです。
では，なぜ（Ａ）が成り立つのかというと，
q^2 が2の倍数ということは，
q×q が2でわり切れるということですが，
２は素数なので，q自体が2で割り切れる数でなくてはならないからなのです。
（これは，実はユークリッドの補題の特殊な場合になっています。）
別の言い方をすれば，qを素因数分解したときに2が素因数になければ，q×qを素因数分解しても2は現れないことになってしまうから，q×qが2を素因数としてもつなら，q自体も2を素因数として持っていなければならないということです。
一方，素数ではない４の場合はこの理屈は通用しません。
なぜなら，
q×q が４でわり切れたとしても，qは２で割り切れる数であれば十分だからです。
実際，q=6 だったとすると，qは４でわり切れませんが，q×q=36 は４で割り切れる数になっていますね。
この隠されたカギを理解しておかないと，本当の意味でルート２が無理数であることを理解できたことにはならないのではないでしょうか。
注）q×q が２の倍数ということは，q×q が偶数ということです。
偶数×偶数＝偶数，奇数×奇数＝奇数
なのでq は偶数でなくてはならない，と理解することもできますが，本質はやはり２が素数だからという点でしょう。その本質を理解することで，２だけではなく，他の素数の平方根が無理数であることも同様に証明できることになるのです。
背理法による証明が有名だと思いますが，その証明の中で次のような説明を目にすると思います。
「q^2は２の倍数。よってqも２の倍数。」
※q^2はqの２乗の意味
これは，教科書などに載っている証明でもこのように書かれているのですが，次のサイトから引用しました：
https://mathtrain.jp/sqrt2irrational
私が高校生の時，この証明を見て
えっ，なんでqも２の倍数なの？？
と思ったことを今でも覚えているのですが，みなさんも疑問に思ったことはないでしょうか？
さらっと「よってqも２の倍数」と説明もなく書かれていますが，実はこの部分にこそ，ルート２が無理数であることを示す重要なカギが隠れているんです。
少し考えてみましょう。
「q^2は２の倍数。よってqも２の倍数。」・・・（Ａ）
では，
「q^2は４の倍数。よってqも４の倍数。」・・・（Ｂ）
も成り立つのでしょうか？
答えはもちろんＮＯです。
似たような推論なのに，（Ａ）は成り立ちますが，（Ｂ）は成り立たないんです。
もし仮に（Ｂ）が成り立てば，ルート２が無理数であることと全く同じ証明で，ルート４が無理数であることを示せることになってしまいます。
もちろんルート４は２ですから，そんなことがあってはおかしいのです。
ではなぜ（Ａ）が成り立つのかというと，２が素数だからなんです。
（Ａ）の推論の中に隠されていたカギを付け足して書き直すと，
「q^2は２の倍数。２は素数なので，qも２の倍数でなくてはならない。」・・・（Ａ'）
ということなんです。
２が素数だからこの推論は正しくて，逆に４は素数ではないから（Ｂ）は正しくない。
だからルート４に対してはこの証明法は使えないんです。
では，なぜ（Ａ）が成り立つのかというと，
q^2 が2の倍数ということは，
q×q が2でわり切れるということですが，
２は素数なので，q自体が2で割り切れる数でなくてはならないからなのです。
（これは，実はユークリッドの補題の特殊な場合になっています。）
別の言い方をすれば，qを素因数分解したときに2が素因数になければ，q×qを素因数分解しても2は現れないことになってしまうから，q×qが2を素因数としてもつなら，q自体も2を素因数として持っていなければならないということです。
一方，素数ではない４の場合はこの理屈は通用しません。
なぜなら，
q×q が４でわり切れたとしても，qは２で割り切れる数であれば十分だからです。
実際，q=6 だったとすると，qは４でわり切れませんが，q×q=36 は４で割り切れる数になっていますね。
この隠されたカギを理解しておかないと，本当の意味でルート２が無理数であることを理解できたことにはならないのではないでしょうか。
注）q×q が２の倍数ということは，q×q が偶数ということです。
偶数×偶数＝偶数，奇数×奇数＝奇数
なのでq は偶数でなくてはならない，と理解することもできますが，本質はやはり２が素数だからという点でしょう。その本質を理解することで，２だけではなく，他の素数の平方根が無理数であることも同様に証明できることになるのです。
無理数は有理数よりも遥かに多い？【カントルの対角線論法】 [数学研究室【一般向け】]
これまで集合論に関して，なるべく分かりやすく記事を書いてきましたが，今回はひとつの区切りというかゴールになるのではないかと思います。
つまり，無理数は有理数よりももっと多く存在しているという事についてです。
この事は，1874年にカントルよって区間縮小法に基づく背理法で証明されたのですが，後に有名な対角線論法により，自身で改めて証明をし直したそうです。
数直線上の点はすべてある実数を表しています。
実数は分数で表すことのできる有理数と，分数で表すことのできない無理数とでできています。
数直線は有理数の点でびっしりと埋め尽くされているのですが，それにも関わらず，無理数は有理数よりももっと高い濃度で数直線上に存在しているのです。
数直線は有理数の点と無理数の点の集まりでできています。そもそも不可能な話ですが，例えば０から１の間の数直線を，有理数の点と無理数の点に分けることができたとしましょう。有理数の点だけでも無限にあるのですが，実は無理数の点はそれ以上に多く存在しているということです。
このことは，無限にも階級（ランク）のようなものがあるという事を示しています。
簡単に言えば，順番を付けて並べることができるような無限を「可算無限」，順番を付けて並べることができない無限を「非可算無限」と言い，有理数点は可算無限であるのに対し，無理数点は非可算無限であるということです。可算無限は例えば偶数全体のように，１つひとつの元に順番をつけて無限に並べることができますが，非可算無限はまるで液体のように，１粒１粒並べたとしても，粒がさらに細かく分かれて並べることが出来ないようなものなのです。
記事ですべてを書くことは大変でしたので，プリントにしましたが，なるべく分かりやすく書いたつもりですので，ぜひご一読いただいて，無限の不思議を少しでも読者の皆さまと共有できたらと思います。
無理数の濃度(Page 1)
無理数の濃度(Page 2)
※本記事から初めて読むと難しと思いますので，以下の関連記事を上から順に読んでいただけると，より内容が理解できるかなと思います。
＜YouTubeチャンネル＞
＜関連記事＞
⇒偶数と整数は同じ個数？
⇒有理数と整数は同じ個数？
⇒整数を無限小数で表す【無限小数展開】
⇒実数全体も０から１の間の実数も濃度は一緒？
つまり，無理数は有理数よりももっと多く存在しているという事についてです。
この事は，1874年にカントルよって区間縮小法に基づく背理法で証明されたのですが，後に有名な対角線論法により，自身で改めて証明をし直したそうです。
数直線上の点はすべてある実数を表しています。
実数は分数で表すことのできる有理数と，分数で表すことのできない無理数とでできています。
数直線は有理数の点でびっしりと埋め尽くされているのですが，それにも関わらず，無理数は有理数よりももっと高い濃度で数直線上に存在しているのです。
数直線は有理数の点と無理数の点の集まりでできています。そもそも不可能な話ですが，例えば０から１の間の数直線を，有理数の点と無理数の点に分けることができたとしましょう。有理数の点だけでも無限にあるのですが，実は無理数の点はそれ以上に多く存在しているということです。
このことは，無限にも階級（ランク）のようなものがあるという事を示しています。
簡単に言えば，順番を付けて並べることができるような無限を「可算無限」，順番を付けて並べることができない無限を「非可算無限」と言い，有理数点は可算無限であるのに対し，無理数点は非可算無限であるということです。可算無限は例えば偶数全体のように，１つひとつの元に順番をつけて無限に並べることができますが，非可算無限はまるで液体のように，１粒１粒並べたとしても，粒がさらに細かく分かれて並べることが出来ないようなものなのです。
記事ですべてを書くことは大変でしたので，プリントにしましたが，なるべく分かりやすく書いたつもりですので，ぜひご一読いただいて，無限の不思議を少しでも読者の皆さまと共有できたらと思います。
無理数の濃度(Page 1)
無理数の濃度(Page 2)
※本記事から初めて読むと難しと思いますので，以下の関連記事を上から順に読んでいただけると，より内容が理解できるかなと思います。
＜YouTubeチャンネル＞
＜関連記事＞
⇒偶数と整数は同じ個数？
⇒有理数と整数は同じ個数？
⇒整数を無限小数で表す【無限小数展開】
⇒実数全体も０から１の間の実数も濃度は一緒？
タグ：無限
2018年09月18日のつぶやき 2018/09/19
motaco0925チョコレートをバラバラにするには何回割ればいいか考える問題。シンプルな... https://t.co/nUN4HqYgBE09/18 20:48
