チョコレートを割る回数【視点を変えてスッキリ解決!】 [算数研究室【小学生向け】]
小学生向けの問題ですが,意外と大人でも気づかないとその法則に気づかない問題です。
問題:次のチョコレートをバラバラにするには,何回割ればいいですか? ただし,2枚以上重ねて折ってはいけません。

横に切れ目が4本,縦に切れ目が5本ありますね。
ですが,切れ目に注目しているとなかなかその法則には気づきません。
下の方に解答を載せておきますので,ぜひ皆さん考えてみてくださいね!
※チョコレートの画像はインターネット上自由に改変・再使用が認められているものを使用しています。
*YouTubeチャンネル*
*解答*
チョコは1回割るごとに,枚数が1枚ずつ増えていきます。
縦に5個,横に6個チョコが並んでいるので,全部で5×6=30(個)に分ければいいので,
30-1=29
で29回割る必要があります。
問題:次のチョコレートをバラバラにするには,何回割ればいいですか? ただし,2枚以上重ねて折ってはいけません。

横に切れ目が4本,縦に切れ目が5本ありますね。
ですが,切れ目に注目しているとなかなかその法則には気づきません。
下の方に解答を載せておきますので,ぜひ皆さん考えてみてくださいね!
※チョコレートの画像はインターネット上自由に改変・再使用が認められているものを使用しています。
*YouTubeチャンネル*
*解答*
チョコは1回割るごとに,枚数が1枚ずつ増えていきます。
縦に5個,横に6個チョコが並んでいるので,全部で5×6=30(個)に分ければいいので,
30-1=29
で29回割る必要があります。
ブログの名称変更 [その他の話]
この度,ブログの名称を
「如月博士のさんすう教室」
から
「もたこ博士のさんすう工房」
へと変更いたしました。
「如月」というと,いまいち読み方が分からなかったり堅苦しい感じがしたりして,もっと親しみやすい名称が良いかと思い,変更しました。
今後もどうぞよろしくお願いいたします![[グッド(上向き矢印)]](https://blog.ss-blog.jp/_images_e/145.gif)
「如月博士のさんすう教室」
から
「もたこ博士のさんすう工房」
へと変更いたしました。
「如月」というと,いまいち読み方が分からなかったり堅苦しい感じがしたりして,もっと親しみやすい名称が良いかと思い,変更しました。
今後もどうぞよろしくお願いいたします
実数全体も0から1の間の実数も濃度は一緒?【数の不思議】 [数学研究室【一般向け】]
実数の濃度に関して,非常に面白い事実があります。
0 < x < 1 を満たす実数 x の範囲を,区間 (0,1) と表します。
さて,区間 (0,1) には一体どれほどの実数が含まれているのでしょうか?
0.1
0.001
0.21647
などなど,区間 (0,1) だけとっても,無数に実数が含まれているわけです。
では,区間 (0,2) と比べてみましょう。
単純に区間が2倍になったので,2倍の量の実数が含まれているような気がしますよね?
ですが,その直観は残念ながら外れているのです。
〇区間(0,1)と区間(0,2)の実数の個数
次の図を見てください。
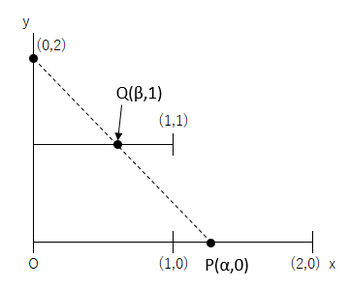
点Pに対して,点Qがただ1つ定まります。
点Pの x 座標 α は区間 (0,2) の実数ですが,それに対応して点Qの x 座標 β ∈ (0,1)が定まります。
この対応は,区間 (0,2) と区間 (0,1) の1対1対応を与えていますので,区間 (0,1) の実数の個数と区間 (0,2) の実数の個数は等しいということになります。
区間 (0,1) も区間 (0,2) も集合としては無限集合ですので,より正確には2つの集合の濃度は等しいということになります。
〇区間(0,1)の実数と実数全体
さらに不思議なことに,区間 (0,1) に含まれる実数と,数直線全体に含まれる実数全体の濃度ですら,実は等しくなります。
区間 (0,1) の実数と,正の実数 (0,+∞) は次のように1対1に対応させることができます。
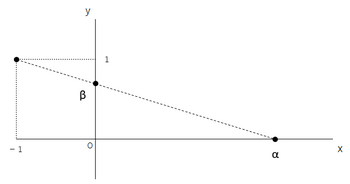
この図のように,xy平面において,任意の実数 α に対してx軸上に点(α,0)をとり,そのと点と点(-1,1)を結ぶ直線をひきます。この直線とy軸との交点を (0,β) とします。
この対応によって,(0,+∞)の実数αに対して(0,1)の実数βが定まります。
逆にβが定まればαもただ1つ定まり,この対応は α∈(0,+∞) とβ∈ (0,1) の1対1対応を与えています。
よって,区間 (0,1) に含まれる実数の濃度と,区間 (0,+∞) に含まれる実数の濃度は等しいということが分かりました。
ここでは簡単に正の実数全体 (0,+∞) と区間 (0,1) の実数を対応させましたが,ここから少し考えれば実数全体 (-∞,+∞) と区間 (0,1) の1対1対応も作ることができます。
無限の世界では,直観では信じられないようなことが起きます。
これは大学1年くらいの集合論の基礎で学びますが,いまだに本当に不思議だと思います。
0 < x < 1 を満たす実数 x の範囲を,区間 (0,1) と表します。
さて,区間 (0,1) には一体どれほどの実数が含まれているのでしょうか?
0.1
0.001
0.21647
などなど,区間 (0,1) だけとっても,無数に実数が含まれているわけです。
では,区間 (0,2) と比べてみましょう。
単純に区間が2倍になったので,2倍の量の実数が含まれているような気がしますよね?
ですが,その直観は残念ながら外れているのです。
〇区間(0,1)と区間(0,2)の実数の個数
次の図を見てください。

点Pに対して,点Qがただ1つ定まります。
点Pの x 座標 α は区間 (0,2) の実数ですが,それに対応して点Qの x 座標 β ∈ (0,1)が定まります。
この対応は,区間 (0,2) と区間 (0,1) の1対1対応を与えていますので,区間 (0,1) の実数の個数と区間 (0,2) の実数の個数は等しいということになります。
区間 (0,1) も区間 (0,2) も集合としては無限集合ですので,より正確には2つの集合の濃度は等しいということになります。
〇区間(0,1)の実数と実数全体
さらに不思議なことに,区間 (0,1) に含まれる実数と,数直線全体に含まれる実数全体の濃度ですら,実は等しくなります。
区間 (0,1) の実数と,正の実数 (0,+∞) は次のように1対1に対応させることができます。

この図のように,xy平面において,任意の実数 α に対してx軸上に点(α,0)をとり,そのと点と点(-1,1)を結ぶ直線をひきます。この直線とy軸との交点を (0,β) とします。
この対応によって,(0,+∞)の実数αに対して(0,1)の実数βが定まります。
逆にβが定まればαもただ1つ定まり,この対応は α∈(0,+∞) とβ∈ (0,1) の1対1対応を与えています。
よって,区間 (0,1) に含まれる実数の濃度と,区間 (0,+∞) に含まれる実数の濃度は等しいということが分かりました。
ここでは簡単に正の実数全体 (0,+∞) と区間 (0,1) の実数を対応させましたが,ここから少し考えれば実数全体 (-∞,+∞) と区間 (0,1) の1対1対応も作ることができます。
無限の世界では,直観では信じられないようなことが起きます。
これは大学1年くらいの集合論の基礎で学びますが,いまだに本当に不思議だと思います。
タグ:無限
吉澤ひとみさんのひき逃げ事件で思うこと [その他の話]
フライデーで,吉澤ひとみさんの飲酒運転によるひき逃げ事件の動画が公開されましたが,みなさんもご覧になりましたでしょうか?
おそらく歩道の信号が青になったのでしょう。
自転車が走り出したところに吉澤ひとみさんの車が突っ込み,自転車の前輪部分に衝突している様子がよく分かります。
そこで思うのですが,何でそんな都合よく動画が出てくるのか?
車が事故を起こす瞬間なんて,いつ起こるか分からないのですから,都合よく動画なんて撮れません。
おそらく車載カメラか何かではないかと思いますが,こんなに都合よく動画が出てくると,
外出しているときには常に誰かに撮影されているのではないか
などと思ってしまいます。
次に思うことは,結構な勢いで車が自転車に突っ込んでいるように見えますが,歩行者や自転車に乗っていた人はなぜ気づかなかったのか?ということです。
普通の感覚として,横断歩道を渡るときには左右を確認するものです。
普通に確認していればあの事故は起きなかったはずです。
もちろん,悪いのは吉澤ひとみ容疑者であることに異論はありませんが,それとは別の問題として,歩行者はもっと安全確認をするべきであると思います。
法的には,当然守られるのは歩行者の方です。
しかし,だからといって自分が車にひかれて良いことにはならないのです。
法的に守られているから,事故にあって障害が残っても良いのか? 事故にあって死んでしまっても良いのか?
車道の信号が黄色から赤になりかけているのにスピードを上げて通ろうとする車がいます。
一方,もう歩道の信号は青になるからと,左右の安全確認もせずにスマートフォンを見ながら横断歩道を渡り始める人がいます。
そりゃあ事故が起きて当然です。
しかし,防げる事故は防ぐべきなんです。
横断歩道を渡るときは,右を見て左を見て,もう一度右を見て渡り始める。
小学校で習わなかったのでしょうか。
おそらく歩道の信号が青になったのでしょう。
自転車が走り出したところに吉澤ひとみさんの車が突っ込み,自転車の前輪部分に衝突している様子がよく分かります。
そこで思うのですが,何でそんな都合よく動画が出てくるのか?
車が事故を起こす瞬間なんて,いつ起こるか分からないのですから,都合よく動画なんて撮れません。
おそらく車載カメラか何かではないかと思いますが,こんなに都合よく動画が出てくると,
外出しているときには常に誰かに撮影されているのではないか
などと思ってしまいます。
次に思うことは,結構な勢いで車が自転車に突っ込んでいるように見えますが,歩行者や自転車に乗っていた人はなぜ気づかなかったのか?ということです。
普通の感覚として,横断歩道を渡るときには左右を確認するものです。
普通に確認していればあの事故は起きなかったはずです。
もちろん,悪いのは吉澤ひとみ容疑者であることに異論はありませんが,それとは別の問題として,歩行者はもっと安全確認をするべきであると思います。
法的には,当然守られるのは歩行者の方です。
しかし,だからといって自分が車にひかれて良いことにはならないのです。
法的に守られているから,事故にあって障害が残っても良いのか? 事故にあって死んでしまっても良いのか?
車道の信号が黄色から赤になりかけているのにスピードを上げて通ろうとする車がいます。
一方,もう歩道の信号は青になるからと,左右の安全確認もせずにスマートフォンを見ながら横断歩道を渡り始める人がいます。
そりゃあ事故が起きて当然です。
しかし,防げる事故は防ぐべきなんです。
横断歩道を渡るときは,右を見て左を見て,もう一度右を見て渡り始める。
小学校で習わなかったのでしょうか。
有理数全体と整数全体の集合について【動画をアップしました】 [その他の話]
以前,記事で書いた内容なのですが,改めて動画での解説を付けましたのでお知らせします。
有理数全体と整数全体は同じ濃度の集合であるということの解説です。
有理数全体と整数全体は同じ濃度の集合であるということの解説です。
なぜ1は素数ではないか?【素因数分解】 [算数研究室【小学生向け】]
1とその数自身以外に約数を持たない整数を素数と言います。
例えば,5は1と5以外では割り切れないので素数ですね。
素数を小さい順に並べると,
2,3,5,7,11,13,17,19,・・・
となりますが,通常1は素数とはしません。
1は,1とその数(1自身)以外に約数を持たないのですから,定義に当てはまっていると言えば当てはまっているのです。
では,なぜ1は素数としないのでしょうか?
良くある解釈としては,
「約数が2つある整数が素数であって,1は約数が1つしかないから素数ではない」
というものだ。
もちろん,そう解釈しても間違いではないとは思います。
しかし,1を素数としない本当の理由は他にあります。
本来の素数の意味を考えれみると,1を素数としない理由が見えてきます。
〇素因数分解
素数以外の整数を,いくつかの整数の積に分けてみます。
例えば,
6=2×3
とできます。12であれば,
12=2×6
となりますが,6はさらに2×3に分けられるので,
12=2×6=2×2×3
と分解できます。
このように,整数を素数の積で表すことを「素因数分解」と言います。
2=2
3=3
4=2×2
5=5
6=2×3
7=7
8=2×2×2
9=3×3
10=2×5
のように,1以外のすべての整数は素数の積で表現できるのです。
そういう意味で,かけ算の世界では,素数はすべての整数の素(もと)と言えるのです。
素因数分解することで,その整数がどのような整数なのかが見えてきます。
例えば,その整数がどのような数で割り切れるのかが分かるので,その数の約数が分かり,さらに約数の個数も素因数分解を見ると計算で求めることができます。
〇素因数分解の一意性
ある物事がただ1つに決まることを一意的と言います。
かけ算の世界では交換法則があるので,2×3も3×2も等しく,かける順番には意味がありません。なので,a×bもb×aも同じと考え,かける順番を無視すれば素因数分解は一意的に決まることになります。
例えば,
12=2×2×3
以外に,12の素因数分解はないのです。
では仮に1を素数としたらどうなるでしょう?
12=1×2×2×3
12=1×1×2×2×3
のように,12の素因数分解が何通りもできてしまうことになります。
このような事が起きないよう,1は素数としないことになっているのです。
また,素数はかけ算の世界では「数の素(もと)」となる数です。
1以外のすべての整数は,素因数分解によって素数の積で表現できるのですが,1は何回かけても変わらないので,他の数を生み出すことはできなません。
そういう意味で,1は数の素とはなれないので,素数の仲間に入れないと考えることもできます。
1はかけ算の世界では,かけてもかけても何も変化を起こさない特殊な数なのですね。
例えば,5は1と5以外では割り切れないので素数ですね。
素数を小さい順に並べると,
2,3,5,7,11,13,17,19,・・・
となりますが,通常1は素数とはしません。
1は,1とその数(1自身)以外に約数を持たないのですから,定義に当てはまっていると言えば当てはまっているのです。
では,なぜ1は素数としないのでしょうか?
良くある解釈としては,
「約数が2つある整数が素数であって,1は約数が1つしかないから素数ではない」
というものだ。
もちろん,そう解釈しても間違いではないとは思います。
しかし,1を素数としない本当の理由は他にあります。
本来の素数の意味を考えれみると,1を素数としない理由が見えてきます。
〇素因数分解
素数以外の整数を,いくつかの整数の積に分けてみます。
例えば,
6=2×3
とできます。12であれば,
12=2×6
となりますが,6はさらに2×3に分けられるので,
12=2×6=2×2×3
と分解できます。
このように,整数を素数の積で表すことを「素因数分解」と言います。
2=2
3=3
4=2×2
5=5
6=2×3
7=7
8=2×2×2
9=3×3
10=2×5
のように,1以外のすべての整数は素数の積で表現できるのです。
そういう意味で,かけ算の世界では,素数はすべての整数の素(もと)と言えるのです。
素因数分解することで,その整数がどのような整数なのかが見えてきます。
例えば,その整数がどのような数で割り切れるのかが分かるので,その数の約数が分かり,さらに約数の個数も素因数分解を見ると計算で求めることができます。
〇素因数分解の一意性
ある物事がただ1つに決まることを一意的と言います。
かけ算の世界では交換法則があるので,2×3も3×2も等しく,かける順番には意味がありません。なので,a×bもb×aも同じと考え,かける順番を無視すれば素因数分解は一意的に決まることになります。
例えば,
12=2×2×3
以外に,12の素因数分解はないのです。
では仮に1を素数としたらどうなるでしょう?
12=1×2×2×3
12=1×1×2×2×3
のように,12の素因数分解が何通りもできてしまうことになります。
このような事が起きないよう,1は素数としないことになっているのです。
また,素数はかけ算の世界では「数の素(もと)」となる数です。
1以外のすべての整数は,素因数分解によって素数の積で表現できるのですが,1は何回かけても変わらないので,他の数を生み出すことはできなません。
そういう意味で,1は数の素とはなれないので,素数の仲間に入れないと考えることもできます。
1はかけ算の世界では,かけてもかけても何も変化を起こさない特殊な数なのですね。
整数を無限小数で表す【無限小数展開】 [数学研究室【一般向け】]
以前の記事で,偶数全体や奇数全体,有理数全体は整数(または自然数)全体と同じ個数(濃度)であることを紹介してきました。
⇒【偶数と整数は同じ個数?】
⇒【有理数と整数は同じ個数?】
そこで,整数や有理数よりももっと多く存在する数として,無理数があることを軽く触れました。
分数で表すことのできる数である有理数は,数直線上びっしりと詰まっているのですが,それよりも高い濃度で無理数は数直線上に敷き詰まっているといったイメージです。
このことを示すのに,無限小数展開を先に紹介した方が都合がよいので,以下プリントにまとめて紹介させていただきます。
また,実数と有理数・無理数の関係もまとめておきましたので,ご覧いただければと思います。

無限小数展開(実数と有理数・無理数)1ページ目

無限小数展開(実数と有理数・無理数)2ページ目
これらを踏まえて,次回以降,無理数が有理数よりももっと高い濃度で数直線上に存在していることをご紹介できればと思います。
<関連記事>
⇒【偶数と整数は同じ個数?】
⇒【有理数と整数は同じ個数?】
⇒【無限小数と極限の関係】
⇒【偶数と整数は同じ個数?】
⇒【有理数と整数は同じ個数?】
そこで,整数や有理数よりももっと多く存在する数として,無理数があることを軽く触れました。
分数で表すことのできる数である有理数は,数直線上びっしりと詰まっているのですが,それよりも高い濃度で無理数は数直線上に敷き詰まっているといったイメージです。
このことを示すのに,無限小数展開を先に紹介した方が都合がよいので,以下プリントにまとめて紹介させていただきます。
また,実数と有理数・無理数の関係もまとめておきましたので,ご覧いただければと思います。

無限小数展開(実数と有理数・無理数)1ページ目

無限小数展開(実数と有理数・無理数)2ページ目
これらを踏まえて,次回以降,無理数が有理数よりももっと高い濃度で数直線上に存在していることをご紹介できればと思います。
<関連記事>
⇒【偶数と整数は同じ個数?】
⇒【有理数と整数は同じ個数?】
⇒【無限小数と極限の関係】
タグ:無限
一次方程式の解はなぜひとつ?【当たり前を問う】 [数学研究室【一般向け】]
一次方程式は一般に
ax+b=0
という形をしています。
xが未知数,aとbは係数です。
係数は整数でも,実数でも複素数でもなんでもいいのですが,a=0だと一次方程式にはなりませんので,a=0ではないとします。
解は,x=-a/b で求められるのですが,では,
「本当に他に解はないのですか?」
と言ったら,きちんと説明できるでしょうか?
一次方程式なんだから解は1つでしょと思われるでしょうが,
では,一次方程式だとなぜ解は1つなのか?
当たり前のことでも根本に戻って考える事が,さらに発展的な思考に結びつきます。
〇当たり前を問う
例えば,2x+1=0の解は,x=-1/2 ですが,本当に他に解がないことが言えるのかということです。
一般に,解が1つ見つかったところで,それで他に解が存在しないとは言い切れません。
実際,二次方程式になると,x^2=4 (x^2はxの2乗)の解は,x=2 ですが,他にも解 x=-2 があるわけですよね。
つまり,方程式は一般には,
「解が見つかった」
ということと,
「解が他にはない」
ということは直接的には結びつかないのです。
では改めて,なぜ一次方程式だと解は1つしかないと言えるのか。
そんなに難しいことはありませんので,ぜひ皆さんも考えてみてくださいね。
考え方は様々あると思いますが,一例をプリントにまとめましたので,ご覧いただければと思います。


ax+b=0
という形をしています。
xが未知数,aとbは係数です。
係数は整数でも,実数でも複素数でもなんでもいいのですが,a=0だと一次方程式にはなりませんので,a=0ではないとします。
解は,x=-a/b で求められるのですが,では,
「本当に他に解はないのですか?」
と言ったら,きちんと説明できるでしょうか?
一次方程式なんだから解は1つでしょと思われるでしょうが,
では,一次方程式だとなぜ解は1つなのか?
当たり前のことでも根本に戻って考える事が,さらに発展的な思考に結びつきます。
〇当たり前を問う
例えば,2x+1=0の解は,x=-1/2 ですが,本当に他に解がないことが言えるのかということです。
一般に,解が1つ見つかったところで,それで他に解が存在しないとは言い切れません。
実際,二次方程式になると,x^2=4 (x^2はxの2乗)の解は,x=2 ですが,他にも解 x=-2 があるわけですよね。
つまり,方程式は一般には,
「解が見つかった」
ということと,
「解が他にはない」
ということは直接的には結びつかないのです。
では改めて,なぜ一次方程式だと解は1つしかないと言えるのか。
そんなに難しいことはありませんので,ぜひ皆さんも考えてみてくださいね。
考え方は様々あると思いますが,一例をプリントにまとめましたので,ご覧いただければと思います。


迷惑な不動産の営業にも意外な一面 [その他の話]
迷惑な訪問としてNHKの集金人や新聞の勧誘,不動産の営業など色々とありますが,私の家にも一度迷惑な不動産の営業が来たことがあります。
ただ,私の場合珍しいことが起きました。
数年前,忘れもしない12月25日です。
世間はクリスマス一色に浮かれている中,私の家のチャイムが鳴りました。
13時頃だったと思います。
出てみると,25歳くらいの短髪で見た目は若干ロックバンドでもやっていたかのような雰囲気のスーツを着た男性だった。
自分がどこの何者かも言わずに,この辺りで住まいに関するお話をさせていただくために訪ねて歩いているのだとか。
「営業なら結構です」と言ったら,
「え,営業なんて言ってないですよね。ちょっとお住まいに関するお話をさせていただいているだけなんですが,それでもだめなんですか?」
「そもそも営業だったとしても,だからといってお話すらさせてもらえないなんて,酷いですよね?」
など,とにかくしつこい。
今となっては,すぐにドアを閉めておけばよかったのですが,迷惑営業が来たのはそれが初めてだったので,少しくらい話を聞こうとすると,いつまでも終わらない。
今後のことを考えると一軒家を買っておいた方がいいだの,一軒家を買ってから引っ越してたとしても,実は損はしないなんだの,一向に終わりの見えない話が続き,
「何の話をしてるんですか? 家なら買う気はありませんよ」
と言っても,
「え,私はただお住まいについてのお話をさせていただいているだけなのですが,家を売りつけているように聞こえました? どうしてそう思ったんですか?」
と,あたかもこちらが悪いことを言ったかのような質問をしてくるので,
「どう見ても営業でしょう。時間がないんで,帰ってもらえますか」
と言うと,
「どうして営業だって決めつけるんですか? そもそも時間がないって,私みたいな人間だと相手にする時間もないっていうんですか?」
と,もはや何を言ってもつっかかってくる。
1時間くらい経った時,もう一人の男性がやってきた。
ちょっと大柄の一見優しそうな雰囲気の人だった。
「すみません。そいつの上司の者ですが,ちょっと時間がかかってると思って様子を見に来ました。もし何か不手際などありましたらすみません」
と言う。
こちらとしては,さっさと帰ってほしいのだが事の顛末を話すと
「なるほど,そいつは新人だったので説明不足などあったかもしれません」
で,また住まいがどうのこうのと,どうでもいい話が始まった。
今の住まいと収入や仕事上の引っ越しの可能性がどうのこうのという話をし出し,
「お仕事は何をされてるんですか?」
と聞かれたので,
「それは個人情報なのでちょっと言えないです」
と言うと,
「え,何で言えないんですか? 職業なんて個人情報じゃないですよ。それとも私たちみたいな人間は信用すらされないから言えないんですか?」
と,つっかかってくる。
もう面倒なので,
「そりゃあそうでしょう。だってあなたたち,自分がどこの会社の者かも言ってないでしょ。そんなどこの誰かも分からない人に自分のこと話せませんよ,もうだいぶ時間も経ってるんで,すみませんが帰ってもらえますか?」
と強めに言うと,態度を一転させ,持っていたバインダーを地面に投げつけ,
「もう客だとか営業だとか関係ない! あなたという人間はとても失礼だ! 出てきて謝りなさい!」
と,キレ出した。
もう相手にするのも面倒になり,当然謝る気もないし,さすがに外に出るのは危ないと思い,
「なんでこっちが謝るんですか。いいから早く帰ってください」
と言うと
「家も買えないような貧乏人なら初めからそう言え!(初めから買う気はないと言っていたのだが)安心してくださいよ,もうこんなとこ来ませんから!」
と捨て台詞を吐いて帰っていったのだ。
時間はすでに2時間半を過ぎていた。
以上が,私が体験した迷惑営業の話です。
ただ,私の場合はまだ良い方で,本当に酷い方の場合は,不動産の営業で5時間以上,夜中の12時まで居座られたという話も聞きます。
で,意外なこととは何だったのかというと,それから1年くらい過ぎたある日,再び家のチャイムが鳴り,出てみると再びあの時の短髪のスーツの男性だった。
今考えると,普通は出ないですよね。
しかし,様子が変だった。
「実は,僕あの会社辞めたんです。それで,今まで回ってたお家に改めてお話が聞きたくって。でも信じてもらえないですかね?」
と言う。話し方も,最初に来た時のような嫌な感じはしなかったが,半分疑いながらもちょっと話を聞いてみると
「もうあんな会社にいるのが嫌になって。あの時どうでした? 正直嫌でしたよね?」
と言うので,
「まあ,普通は嫌ですよね」
と返す。
「あ~,やっぱりそうですよね。自分が今までお伺いしてきた方に,あの時どう思っていたのか知りたくって,今こうして回ってるんです。人に嫌われることばっかりするこんな仕事が嫌になって,もうあの仕事を辞めたんです」
と,どこかさっぱりしたような様子で話し,
「本当にあの時は申し訳なかったなと思いまして・・・すみません。もう帰りますね。ありがとうございました」
と,帰っていった。
以前居座られた記憶から,また居座られたら嫌だなという気持ちもあり,
「そうですか」
としか返せませんでしたが,迷惑な営業の仕事をしている人の中にも,本音ではそんなことをしたくないと思っている人もいるのだと,意外な一面を見た気がしました。
すんなり帰って行って,その後も何もなかったので,本当に嫌になって仕事を辞めたのだと思います。
その時は言えませんでしたが,
「これから頑張って」
とエールを送りたい気持ちにすらなりました。
ただ,私の場合珍しいことが起きました。
数年前,忘れもしない12月25日です。
世間はクリスマス一色に浮かれている中,私の家のチャイムが鳴りました。
13時頃だったと思います。
出てみると,25歳くらいの短髪で見た目は若干ロックバンドでもやっていたかのような雰囲気のスーツを着た男性だった。
自分がどこの何者かも言わずに,この辺りで住まいに関するお話をさせていただくために訪ねて歩いているのだとか。
「営業なら結構です」と言ったら,
「え,営業なんて言ってないですよね。ちょっとお住まいに関するお話をさせていただいているだけなんですが,それでもだめなんですか?」
「そもそも営業だったとしても,だからといってお話すらさせてもらえないなんて,酷いですよね?」
など,とにかくしつこい。
今となっては,すぐにドアを閉めておけばよかったのですが,迷惑営業が来たのはそれが初めてだったので,少しくらい話を聞こうとすると,いつまでも終わらない。
今後のことを考えると一軒家を買っておいた方がいいだの,一軒家を買ってから引っ越してたとしても,実は損はしないなんだの,一向に終わりの見えない話が続き,
「何の話をしてるんですか? 家なら買う気はありませんよ」
と言っても,
「え,私はただお住まいについてのお話をさせていただいているだけなのですが,家を売りつけているように聞こえました? どうしてそう思ったんですか?」
と,あたかもこちらが悪いことを言ったかのような質問をしてくるので,
「どう見ても営業でしょう。時間がないんで,帰ってもらえますか」
と言うと,
「どうして営業だって決めつけるんですか? そもそも時間がないって,私みたいな人間だと相手にする時間もないっていうんですか?」
と,もはや何を言ってもつっかかってくる。
1時間くらい経った時,もう一人の男性がやってきた。
ちょっと大柄の一見優しそうな雰囲気の人だった。
「すみません。そいつの上司の者ですが,ちょっと時間がかかってると思って様子を見に来ました。もし何か不手際などありましたらすみません」
と言う。
こちらとしては,さっさと帰ってほしいのだが事の顛末を話すと
「なるほど,そいつは新人だったので説明不足などあったかもしれません」
で,また住まいがどうのこうのと,どうでもいい話が始まった。
今の住まいと収入や仕事上の引っ越しの可能性がどうのこうのという話をし出し,
「お仕事は何をされてるんですか?」
と聞かれたので,
「それは個人情報なのでちょっと言えないです」
と言うと,
「え,何で言えないんですか? 職業なんて個人情報じゃないですよ。それとも私たちみたいな人間は信用すらされないから言えないんですか?」
と,つっかかってくる。
もう面倒なので,
「そりゃあそうでしょう。だってあなたたち,自分がどこの会社の者かも言ってないでしょ。そんなどこの誰かも分からない人に自分のこと話せませんよ,もうだいぶ時間も経ってるんで,すみませんが帰ってもらえますか?」
と強めに言うと,態度を一転させ,持っていたバインダーを地面に投げつけ,
「もう客だとか営業だとか関係ない! あなたという人間はとても失礼だ! 出てきて謝りなさい!」
と,キレ出した。
もう相手にするのも面倒になり,当然謝る気もないし,さすがに外に出るのは危ないと思い,
「なんでこっちが謝るんですか。いいから早く帰ってください」
と言うと
「家も買えないような貧乏人なら初めからそう言え!(初めから買う気はないと言っていたのだが)安心してくださいよ,もうこんなとこ来ませんから!」
と捨て台詞を吐いて帰っていったのだ。
時間はすでに2時間半を過ぎていた。
以上が,私が体験した迷惑営業の話です。
ただ,私の場合はまだ良い方で,本当に酷い方の場合は,不動産の営業で5時間以上,夜中の12時まで居座られたという話も聞きます。
で,意外なこととは何だったのかというと,それから1年くらい過ぎたある日,再び家のチャイムが鳴り,出てみると再びあの時の短髪のスーツの男性だった。
今考えると,普通は出ないですよね。
しかし,様子が変だった。
「実は,僕あの会社辞めたんです。それで,今まで回ってたお家に改めてお話が聞きたくって。でも信じてもらえないですかね?」
と言う。話し方も,最初に来た時のような嫌な感じはしなかったが,半分疑いながらもちょっと話を聞いてみると
「もうあんな会社にいるのが嫌になって。あの時どうでした? 正直嫌でしたよね?」
と言うので,
「まあ,普通は嫌ですよね」
と返す。
「あ~,やっぱりそうですよね。自分が今までお伺いしてきた方に,あの時どう思っていたのか知りたくって,今こうして回ってるんです。人に嫌われることばっかりするこんな仕事が嫌になって,もうあの仕事を辞めたんです」
と,どこかさっぱりしたような様子で話し,
「本当にあの時は申し訳なかったなと思いまして・・・すみません。もう帰りますね。ありがとうございました」
と,帰っていった。
以前居座られた記憶から,また居座られたら嫌だなという気持ちもあり,
「そうですか」
としか返せませんでしたが,迷惑な営業の仕事をしている人の中にも,本音ではそんなことをしたくないと思っている人もいるのだと,意外な一面を見た気がしました。
すんなり帰って行って,その後も何もなかったので,本当に嫌になって仕事を辞めたのだと思います。
その時は言えませんでしたが,
「これから頑張って」
とエールを送りたい気持ちにすらなりました。
有理数と整数は同じ個数?【いかにして分数を並べるか】 [数学研究室【一般向け】]
前回,偶数と整数は同じ個数であることをご紹介させていただきました。
⇒【偶数と整数は同じ個数?】
正確には,整数全体と偶数全体の濃度が等しいということなのですが,実は有理数(分数で表すことのできる数)全体の濃度も,整数全体の濃度と等しくなります。
本質的には同じなので,ここでは整数や有理数はすべて正の数のみに限定して話を進めていきます。
〇整数全体と同じ濃度(個数)とは?
整数と同じ濃度であるというのは,1から順番に整数を対応させることができるということです。
なので,偶数であれば,小さい順に
2,4,6,8,10,12,・・・
というように並べることができるので,1から順番に整数を対応させることができ,この対応により整数全体と偶数全体は1対1対に対応させることができたのでした。
つまり,整数と同じ濃度であるということは,このように順番をつけて無限に1列に並べることができるということです。
なので,偶数に限らず,3の倍数や5の倍数なども,順番をつけて無限に1列に並べることができるので,整数と同じ濃度を持っています。
〇分数をいかに並べるか
有理数というのは,分数で表すことのできる数です。
偶数や3の倍数などは,小さい順に並べることで自然に1列に並ばせることができるのですが,有理数の場合はそうはいきません。
なぜなら,有理数を小さい順に並べようとしても,最も小さな有理数というのは存在しないからです。
例えば,1/2(2分の1)よりも1/4の方が小さく,さらに1/4よりも1/8の方が小さくなるように,ある有理数があれば,それを半分の大きさにした数もまた有理数だからです。
いくらでも小さな有理数が作れてしまうのですから,有理数を小さい順に並べること自体不可能なのです。
では,どのように有理数を1列に並べるかというと,次のようにします。
1/1 2/1 3/1 4/1 5/1 6/1 ・・・
1/2 2/2 3/2 4/2 5/2 6/2 ・・・
1/3 2/3 3/3 4/3 5/3 6/3 ・・・
1/4 2/4 3/4 4/4 5/4 6/4 ・・・
1/5 2/5 3/5 4/5 5/5 6/5 ・・・
・・・・・・・・・・・・・・
上から1行目には分母が1の分数を,
上から2行目には分母が2の分数を,
上から3行目には分母が3の分数を,
それぞれ小さい順に並べることができますね。
この並びにより,有理数全体を平面上に並べることができます。
では,この並びに対して,整数を次のように割り当てていきます。
1 2 6 7 ・・・
3 5 8 ・・・
4 9 ・・・
10 ・・・
・・・
つまり,左上の1/1からスタートして,この分数を斜めに数えていくということです。
このように分数に順序をつけることで,1番目から順に分数を余すことなく1列に並べることができるのです。
もちろん,約分することで同じ分数になってしまうこともありますが,約分して同じになる分数が出てくれば,それはとばして並べていくことで,重複なく1列に並べることができます。
この並びにより,整数全体と有理数全体は1対1に対応させることができるので,有理数全体と整数全体は同じ濃度であると言えるのです。
このように有理数全体ですら,余すことなくきれいに1列に整列させることができるのですから,もう何でも整数全体と同じ濃度なのではないかと思ってしまいますが,実はより高い濃度の無限集合があるのです。
その集合こそ,無理数全体の集合なのですが,この話はまた次回以降にしたいと思います。
追記:分数の並びが見づらいと思いましたので,プリントにして少し見やすくしました。


*YouTubeチャンネル*
<関連記事>
⇒【偶数と整数は同じ個数?】
⇒【偶数と整数は同じ個数?】
正確には,整数全体と偶数全体の濃度が等しいということなのですが,実は有理数(分数で表すことのできる数)全体の濃度も,整数全体の濃度と等しくなります。
本質的には同じなので,ここでは整数や有理数はすべて正の数のみに限定して話を進めていきます。
〇整数全体と同じ濃度(個数)とは?
整数と同じ濃度であるというのは,1から順番に整数を対応させることができるということです。
なので,偶数であれば,小さい順に
2,4,6,8,10,12,・・・
というように並べることができるので,1から順番に整数を対応させることができ,この対応により整数全体と偶数全体は1対1対に対応させることができたのでした。
つまり,整数と同じ濃度であるということは,このように順番をつけて無限に1列に並べることができるということです。
なので,偶数に限らず,3の倍数や5の倍数なども,順番をつけて無限に1列に並べることができるので,整数と同じ濃度を持っています。
〇分数をいかに並べるか
有理数というのは,分数で表すことのできる数です。
偶数や3の倍数などは,小さい順に並べることで自然に1列に並ばせることができるのですが,有理数の場合はそうはいきません。
なぜなら,有理数を小さい順に並べようとしても,最も小さな有理数というのは存在しないからです。
例えば,1/2(2分の1)よりも1/4の方が小さく,さらに1/4よりも1/8の方が小さくなるように,ある有理数があれば,それを半分の大きさにした数もまた有理数だからです。
いくらでも小さな有理数が作れてしまうのですから,有理数を小さい順に並べること自体不可能なのです。
では,どのように有理数を1列に並べるかというと,次のようにします。
1/1 2/1 3/1 4/1 5/1 6/1 ・・・
1/2 2/2 3/2 4/2 5/2 6/2 ・・・
1/3 2/3 3/3 4/3 5/3 6/3 ・・・
1/4 2/4 3/4 4/4 5/4 6/4 ・・・
1/5 2/5 3/5 4/5 5/5 6/5 ・・・
・・・・・・・・・・・・・・
上から1行目には分母が1の分数を,
上から2行目には分母が2の分数を,
上から3行目には分母が3の分数を,
それぞれ小さい順に並べることができますね。
この並びにより,有理数全体を平面上に並べることができます。
では,この並びに対して,整数を次のように割り当てていきます。
1 2 6 7 ・・・
3 5 8 ・・・
4 9 ・・・
10 ・・・
・・・
つまり,左上の1/1からスタートして,この分数を斜めに数えていくということです。
このように分数に順序をつけることで,1番目から順に分数を余すことなく1列に並べることができるのです。
もちろん,約分することで同じ分数になってしまうこともありますが,約分して同じになる分数が出てくれば,それはとばして並べていくことで,重複なく1列に並べることができます。
この並びにより,整数全体と有理数全体は1対1に対応させることができるので,有理数全体と整数全体は同じ濃度であると言えるのです。
このように有理数全体ですら,余すことなくきれいに1列に整列させることができるのですから,もう何でも整数全体と同じ濃度なのではないかと思ってしまいますが,実はより高い濃度の無限集合があるのです。
その集合こそ,無理数全体の集合なのですが,この話はまた次回以降にしたいと思います。
追記:分数の並びが見づらいと思いましたので,プリントにして少し見やすくしました。


*YouTubeチャンネル*
<関連記事>
⇒【偶数と整数は同じ個数?】



